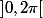Tore et sphère

[barbu23]

Bonsoir à tous : :happy3:
Première question :
Quel'qu'un peut - t - il me rappeler comment decrit - on un tore en geometrie differentielle ? Quel est son equation ? Il y'avait cette ecriture là , je sais pas ou j'l'ai vue : , est ce que vous pouvez me detailler un peu plus cette idée ?
Deuxième question :
Imaginons devant nous une 3 - sphère decrite par son equation : , si on presse lègèrement sur cette sphère, comment devient son equation ? :happy3:
Merci d'avance ! :happy3:

[ludo56]

Salut !
La notation R/Z vient de la topologie. Sans entrer dans les détails,cela signifie que deux éléments de R x et y sont dans la même classe si on peut passer de l'un à l'autre par translation (i.e x=y+n avec n dans Z). Par exemple 0 et 1 sont dans la même classe donc égaux en tant qu'élément de R/Z. A priori R/Z décrit un cercle et non pas un tore.

Je t'aurai bien donner la paramétrisation du tore en géométrie diff mais je sais pas me servir de latex donc galère ! Mais tu dois facilement pouvoir la trouver sur le net !

[Arkhnor]

Salut.

La notation R/Z provient d'abord de l'algèbre. C'est le quotient du groupe additif R par son sous groupe Z, l'ensemble des classes d'équivalence modulo Z.
Comme on a une topologie sur R, on peut munir R/Z de la topologie quotient.
En faisant ça, on obtient quelque chose d'homéomorphe au cercle unité S1.
Il se trouve que le tore à une dimension, et le cercle unité, c'est la même chose.
En dimension supérieure, c'est différent.
On peut toujours quotienter le groupe additif R^n par Z^n, mettre la topologie quotient, et obtient le tore à n dimensions.

Dans R^3, une paramétrisation du tore est donnée par , avec a>b>0 et x et y variant dans

[Pythales]

Moi je veux bien te donner la paramétrisation du tore :



A titre d'exercice, fais une figure et essaye de voir à quoi correspondent , , et