Topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 11 Oct 2007, 17:15
par aviateurpilot » 11 Oct 2007, 17:15
soit
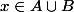
si
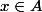
alors
\ge min(inf(A),inf(B)))
si
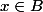
alors
\ge min(inf(A),inf(B)))
donc
,inf(B)))
par suite
\ge min(inf(A),inf(B)))

donne
\ge inf(A\cup B))

donne
\ge inf(A\cup B))
donc
\le min(inf(A),inf(B)))
d'ou
= min(inf(A),inf(B)))
-
minidiane
- Membre Rationnel
- Messages: 678
- Enregistré le: 06 Nov 2006, 18:04
-
 par minidiane » 11 Oct 2007, 17:24
par minidiane » 11 Oct 2007, 17:24
Je pense que les inter son des unions en faite, c'est bien ça?
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 11 Oct 2007, 17:40
par aviateurpilot » 11 Oct 2007, 17:40
minidiane a écrit:Je pense que les inter son des unions en faite, c'est bien ça?
oui, désole
j'ai idité mon poste
-
minidiane
- Membre Rationnel
- Messages: 678
- Enregistré le: 06 Nov 2006, 18:04
-
 par minidiane » 11 Oct 2007, 17:46
par minidiane » 11 Oct 2007, 17:46
ok pas grave merci beaucoup de ton aide
si tu as encore du temps j'aimerai bien une version courte comme celles que m'a faite pour le ii)
Si tu as pas le temps c'est pas grave
merci encore
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 11 Oct 2007, 18:29
par aviateurpilot » 11 Oct 2007, 18:29
préliminaire:
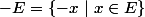
il est evident que
=-inf(-E))
,
=max(-x,-y))
et que
\cup(-B)=-(A\cup B))
et c'est ce que je vais utilisé.
 \\ =-inf(-(A\cup B)) \\ =-inf((-A)\cup (-B))\\ =-min(inf(-A),inf(-B))\\ =max(-inf(-A),-inf(-B))\\=max(sup(A),sup(B)))
-
minidiane
- Membre Rationnel
- Messages: 678
- Enregistré le: 06 Nov 2006, 18:04
-
 par minidiane » 11 Oct 2007, 20:00
par minidiane » 11 Oct 2007, 20:00
Merci beaucoup aviateurpilot, merci à tous ceux qui m'ont aidé merci beaucoup
-
thomasg
- Membre Relatif
- Messages: 443
- Enregistré le: 06 Mai 2005, 09:45
-
 par thomasg » 11 Oct 2007, 20:23
par thomasg » 11 Oct 2007, 20:23
Les démos d'aviateur pilote sont élégantes.
Personnellement j'aime bien les suites ... qui n'ont pas rencontré un franc succés dans cette discussion.
-
minidiane
- Membre Rationnel
- Messages: 678
- Enregistré le: 06 Nov 2006, 18:04
-
 par minidiane » 11 Oct 2007, 20:52
par minidiane » 11 Oct 2007, 20:52
oui j'aime bien ces démonstrations ^^
Perso les suites j'ai du mal
En tout cas merci thomasg quand même t'es toujours là pour m'aider ^^
 par legeniedesalpages » 11 Oct 2007, 20:52
par legeniedesalpages » 11 Oct 2007, 20:52
personnellement, je trouve que les suites sont un outil un peu trop sophistiqué pour ce genre d'exos, j'utilise plutôt la caractérisation séquentielle pour les bornes d'une fonction numérique.
-
minidiane
- Membre Rationnel
- Messages: 678
- Enregistré le: 06 Nov 2006, 18:04
-
 par minidiane » 11 Oct 2007, 21:09
par minidiane » 11 Oct 2007, 21:09
Bonsoir thomasg si tu repasses par là et que tu as un peu de temps j'aimerai savoir comment faire avec les suites pour le dernier cas cela m'interesse quand même ^^
-
thomasg
- Membre Relatif
- Messages: 443
- Enregistré le: 06 Mai 2005, 09:45
-
 par thomasg » 12 Oct 2007, 08:54
par thomasg » 12 Oct 2007, 08:54
C'est fait.
Voir le message #53.
A bientôt.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 12 Oct 2007, 09:18
par aviateurpilot » 12 Oct 2007, 09:18
minidiane a écrit:Bonsoir thomasg si tu repasses par là et que tu as un peu de temps j'aimerai savoir comment faire avec les suites pour le dernier cas cela m'interesse quand même ^^
supposons que
x_n\ge inf(A\cap B))
en particulier on a

and
)
(absurde)
par suite
\ge max(inf(A),inf(B)))
-
minidiane
- Membre Rationnel
- Messages: 678
- Enregistré le: 06 Nov 2006, 18:04
-
 par minidiane » 12 Oct 2007, 12:49
par minidiane » 12 Oct 2007, 12:49
Super merci à vous deux :D
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités