Topologie
73 messages
- Page 3 sur 4 - 1, 2, 3, 4
Si  , comme A et B jouent des rôles symétriques, on peut limiter l'étude au cas où
, comme A et B jouent des rôles symétriques, on peut limiter l'étude au cas où  .
.
en fait on va utiliser la caractérisation séquentielle de la borne inférieure:
il existe une suite) de points de
de points de 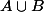 qui a pour limite
qui a pour limite  .
.
Notons .
.
Par définition de la limite, il existe un entier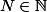 tel que
tel que 
Donc pour tout entier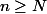 , les termes de cette suite sont dans B, donc
, les termes de cette suite sont dans B, donc  .
.
si , on suppose qu'il existe un point x de
, on suppose qu'il existe un point x de 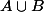 tel que
tel que 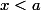 .
.
Donc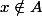 et
et 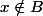 , ce qui est absurde, donc a est un minorant de
, ce qui est absurde, donc a est un minorant de 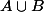 , d'où
, d'où  .
.
en fait on va utiliser la caractérisation séquentielle de la borne inférieure:
il existe une suite
Notons
Par définition de la limite, il existe un entier
Donc pour tout entier
si
Donc
Bonsoir,
cela peut se faire à l'aide de suites comme je l'ai proposé en page 1.
Remarque: comme on travaille dans R le théorème de la borne sup nous dit que tous les sup et inf considérés dans cet exercice existent.
il existe (un), une suite d'éléments de A inter B, qui converge vers inf(A inter B)
cette suite constituée d'éléments de A converge donc nécessairement vers un nombre supérieur ou égal à inf(A). (cela se prouve par l'absurde comme dans mon premier message en page 1)
cette suite constituée d'éléments de B converge donc nécessairement vers un nombre supérieur ou égal à inf(B).
Donc inf(A inter B) supérieur ou égal à inf(A) et inf(B).
A bientôt.
cela peut se faire à l'aide de suites comme je l'ai proposé en page 1.
Remarque: comme on travaille dans R le théorème de la borne sup nous dit que tous les sup et inf considérés dans cet exercice existent.
il existe (un), une suite d'éléments de A inter B, qui converge vers inf(A inter B)
cette suite constituée d'éléments de A converge donc nécessairement vers un nombre supérieur ou égal à inf(A). (cela se prouve par l'absurde comme dans mon premier message en page 1)
cette suite constituée d'éléments de B converge donc nécessairement vers un nombre supérieur ou égal à inf(B).
Donc inf(A inter B) supérieur ou égal à inf(A) et inf(B).
A bientôt.
ok merci thomasg
voici ce que j'ai fait
il existe une suite (xn) appartenant à A qui converge vers x>=inf A
il existe une suite (yn) appartenant à B qui converge vers y>=inf B
Soit zn=xn inter yn, zn appartient donc à A inter B et zn converge vers z>=max(infA, inf B)
D'ou fin(A inter B)>=max(inf a, inf B)
Est-ce bien rédigé?
voici ce que j'ai fait
il existe une suite (xn) appartenant à A qui converge vers x>=inf A
il existe une suite (yn) appartenant à B qui converge vers y>=inf B
Soit zn=xn inter yn, zn appartient donc à A inter B et zn converge vers z>=max(infA, inf B)
D'ou fin(A inter B)>=max(inf a, inf B)
Est-ce bien rédigé?
:we: merci
sinon j'ai du mal avec la première aussi j'ai un truc assez compliqué en fait, voici ce que j'ai:
soit z appartenant A+B implique z=x+y, avec x appartient à A et y appartient à B implique z=x+y<=supA+supB. Donc supa+supB est un majorant pour A+B implique sup(A+B)<=supA+supB
Soit x appartenant à A et y appartenant à B implique x+y appartient à A+B implique x+y<=sup(A+B) équivalent à x<=sup(a+B)-y
Donc sup(A+B)-y est un majorant pour A implique supA<=sup(A+B)-y, quelque soit y appartenant à B. Parce que A est bornée supA<=sup(A+B)-y quelque soit y appartenant à B implique y<=sup(A+B)-supA, quelque soit y appartenant à B implique supB<=sup(A+B)-supA équivalent à supA+supB<=sup(A+B).
On obtient que sup(A+B)=supA+supB.
Voilà je pense qu'il y a plus simple mais j'ai pas trouvé
sinon j'ai du mal avec la première aussi j'ai un truc assez compliqué en fait, voici ce que j'ai:
soit z appartenant A+B implique z=x+y, avec x appartient à A et y appartient à B implique z=x+y<=supA+supB. Donc supa+supB est un majorant pour A+B implique sup(A+B)<=supA+supB
Soit x appartenant à A et y appartenant à B implique x+y appartient à A+B implique x+y<=sup(A+B) équivalent à x<=sup(a+B)-y
Donc sup(A+B)-y est un majorant pour A implique supA<=sup(A+B)-y, quelque soit y appartenant à B. Parce que A est bornée supA<=sup(A+B)-y quelque soit y appartenant à B implique y<=sup(A+B)-supA, quelque soit y appartenant à B implique supB<=sup(A+B)-supA équivalent à supA+supB<=sup(A+B).
On obtient que sup(A+B)=supA+supB.
Voilà je pense qu'il y a plus simple mais j'ai pas trouvé
73 messages
- Page 3 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
