Topologie

[minidiane]

pour la 1ère, je l'ai déja fait dans un post précédent
Pour la 2ème je cherche ...

oops j'avais pas vu désolé merci je vais aller voir
et merci pour la deuxième aussi

[minidiane]

[quote="klevia"]Il me semble que sup(AUB)=max(sup A, sup B)
A C AUB => sup Asup B

cela signifie qu'il existe un intervalle
]sup A-EPsilon, sup A] inter B = ensemble vide
donc soit xn une suite d'élément de AUB convergeant vers sup (AUB)
il existe un rang N où pour tout n>n xn appartient à A
d'ou sup (AUB)supA???
Est-ce que c'est annalogue au premier cas?

[klevia]

ben oui, A ou B c'est pareil ...

[minidiane]

ok merci est-ce que je dois le dire dans la démonstration par exemple si j'ai un exo du même genre en interro est-ce que je dois dire dans le cas où on a supB>supa cela revient au 1er cas ou je n'ai pas besoin de le dire?

[klevia]

Disons que de le dire ne t'enlèvera pas de point alors qu'un prof très tatillon peu raler ...

[minidiane]

ok merci de m'aider
pour la iii) pour l'instant je ne vois pas trop comment faire et pour la iv) et v) je ne trouve pas les relations :briques:

[legeniedesalpages]

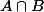
pour la iii), si non vide, je pense qu'il n'y a pas plus à dire que .

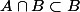
En fait tu vois que et , donc et , d'où la relation.

iv) inf (AUB)

essaie de voir comment par rapport à et .


v) inf(A inter B)

pareil, essaie de voir comment par rapport à et .

[thomasg]

Démo du i/ en première page du post modifiée

[minidiane]

ok merci thomasg
legeniedesalpages j'ai une question pour le iii) si on a A inter B qui est vide que ce passe t-il au niveau du sup?
pour le iv) et le v) pour l'instant je n'ai pas trouvé la relation

[legeniedesalpages]

le sup et le inf ne sont pas définies pour l'ensemble vide, ça n'a pas de sens.
Donc pour ce cas là, il n'y a rien à comparer.

[legeniedesalpages]

pour la iv), il faut penser comme pour la ii).

[minidiane]

Ah oui je comprend je pense que c'est inf(AUB)=min( inf A, inf B)

[legeniedesalpages]

c'est bien ça, reste à reprendre la démo de ii) et l'adapter.

[barbu23]

"legeniedesalpages" est ce que tu peux m'aider sur une question que j'ai posté sur le topic "Calcul differentiel" !!
Merci infiniment !!

[minidiane]

inf(AUB)=min( inf A, inf B)
A C AUB => inf A>= inf AUB (1)

1)supposons inf A>inf B

cela signifie qu'il existe un intervalle
]inf A-Epsilon, inf A] inter B = ensemble vide
donc soit xn une suite d'élément de AUB convergeant vers inf (AUB)
il existe un rang N où pour tout n>n xn appartient à A
d'ou inf (AUB)>= inf A (2)

(1) et (2) inf AUB = inf A

2) si inf A=inf B=l

pour toute suite de AUB convergeant vers inf (AUB)

xn appartient à A ou B d'ou xn<= l d'ou lim xn<=l d'ou inf AUB<= l

J'espère que c'est correct

[legeniedesalpages]

1)supposons inf A>inf B

cela signifie qu'il existe un intervalle
]inf A-Epsilon, inf A] inter B = ensemble vide

si je prends A=[1/2,1] et B=[0,1],

on a bien inf A>inf B, et pourtant on a ]inf A-Epsilon, inf A] inter B = ]1/2-Epsilon, 1/2] inter [0,1] qui est vide seulement pour epsilon=1/2, et je ne vois pas en quoi ça te sert pour la suite.

Plus simplement, on a donc , De plus donc . D'où .

[minidiane]

Ah oui pas besoin d'utiliser de suite dans ce sens alors.
Par contre je suppose qu'après il faut traiter le cas inverse c'est-à-dire: inf (AUB)<=min(inf A, inf B)

[legeniedesalpages]

Ah oui pas besoin d'utiliser de suite dans ce sens alors.
Par contre je suppose qu'après il faut traiter le cas inverse c'est-à-dire: inf (AUB)<=min(inf A, inf B)

c'est pas ce que j'ai fait?

[minidiane]

Ah oui mais je voulai dire min(inf A, inf B)<=inf(AUB)

[legeniedesalpages]

[quote="minidiane"]Ah oui mais je voulai dire min(inf A, inf B)inf AUB et tu montres que inf B <= inf AUB.
Après comme A et B jouent des rôles symétriques, tu en déduis l'inégalité.