Topologie

[shtefi]

Caractérisation des compactes de R (ensemble des réels)

La définition donnée par mon manuel de mathématiques est : une partie K de R est compacte, si et seulement si de toute suite (Un) à valeurs dans K, on peut extraire une sous-suite convergente.

Pour se faire, le manuel suppose K compacte et commence la démonstration en indiquant que K est borné puis se sert naturellement du théorème de Bolzano-Weierstrass pour démontrer que l'on peut extraire une sous-suite de (Un) convergeant vers le point d'accumulation, limite de cette suite.

Or, pour moi, rien ne permet, dans la définition, de supposer que K est borné. En effet, je pensais utiliser la caractérisation des fermés de R afin de démontrer que K est fermé ( donc borné) mais pour cela il faudrait que l'énoncé précise que la limite de (Un) soit dans K. Ce que ne suggère nullement l'énoncé en l'occurance.

La difficulté, à mes yeux, réside donc juste dans la démonstration de K étant borné.

Si quelqu'un peut m'aider sur ce point ou me proposer un autre énoncé (peut-être plus complet) j'en serait très reconnaissant.

Merci d'avance !!!

[quinto]

Bonjour,
en fait je ne comprend pas ta question:
Ton bouquin prend la définition et tu essaies de la démontrer.
Il y'a quelque chose qui cloche.
Que veux tu démontrer, et sinon quelle définition de compact prends tu?

[quinto]

En relisant ce que tu dis, une chose m'interpelle:

"la caractérisation des fermés de R afin de démontrer que K est fermé ( donc borné)"

être fermé dans R ne dit rien sur le fait qu'il soit borné ou non.
Qu'elle est la caractérisation des fermés de R dont tu parles?

"mais pour cela il faudrait que l'énoncé précise que la limite de (Un) soit dans K"

C'est justement ça être fermer.

[khivapia]

Bonsoir tout le monde

en fait tout compact K est borné : si je le recouvre par , je peux en extraire un sous-recouvrement fini par les boules centrées sur des certains (en nombre fini), donc en fait K est inclus dans la boule de rayon (et ce maximum existe car les sont en nombre fini).

Ca c'était une démonstration avec le théorème de Bolzano-Weierstrass.

Aveec la définition : si K n'est pas borné, alors je peux trouver une suite d'éléments de K telle que pour tout n 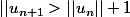. On déduit qu'on ne peut pas extraire de suite convergente de en prenant par exemple 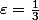et en revenant à la définition de la limite.


Tous les compacts sont donc bornés.

En revanche ce n'est pas le cas des fermés, par exemple n'est pas borné pour la valeur absolue...

[quinto]

En fait tous les compacts sont fermés et bornés, mais l'inverse n'est pas vrai.
Cependant c'est vrai dans R^n, c'est le théorème de Heine-Borel.

[shtefi]

Merci à tous pour votre aide ! :)

[Anonyme]

Il faut dire que si K n'etait pas borné il y aurait une suite qui tendrait vers l'infini et donc on ne en extraire de sous-suite convergente. Donc par l'absurde tout compact de R est borné (et c'est donc une consequence immediate de la definition)