Topologie

[Sam2110]

Salut a tous de l'aide svp

On note E = C([0; 1] ; R) et, pour ϕ ∈ E, Nϕ : E → R l’application définie par :
∀f ∈ E,Nϕ(f)=||fϕ||∞
1.Montrer que Nϕ est une norme sur E si et seulement si ϕ−1({0})= ∅.(intérieur)
2. Montrer que Nϕ et ||•||∞ sont des normes sur E équivalentes si et seulement si ϕ−1({0}) = ∅.

[GaBuZoMeu]

Bonjour,

Qu'as-tu essayé ? Que dois tu vérifier pour montrer que est une norme ? Qu'est-ce qui coince pour toi ?

[Sam2110]

J'ai considéré que Nϕ est une norme pour ensuite montrer que l'intérieur de ϕ−1({0})= ∅.j'arribe pas a cette équivalence


,

[GaBuZoMeu]

Raisonne par l'absurde : suppose qu'il y a un intervalle ouvert non vide contenu dans [0,1] où ne s'annule pas, et alors tu verras je pense sans difficulté qu'il y a une fonction 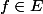non nulle telle que .

[Sam2110]

j'crois toujours pas...
Mon mail : samadoulougouabraham7@gmail.com

[GaBuZoMeu]

J'attends que tu fasses un petit effort.