Bonjour, aidez moi à traiter cet exo:
1) A quelle condition doivent verifier A et B pour que

difinissent une topologie sur E?
2) Determiner si les ensembles suivants sont ou ne sont pas compacts
\in R^2, x^2+y^4=1\})
\in R^2, x^2+y^2 inferieur a 1\})
\in R^2, x\ge 0 et 0\le y \le \frac{1}{x+1} \})
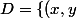\in R^2, y^2 = x(1+2x)\})
.
Mes elements de reponses:
1) On voit que

et

maintenant pour que
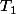
soit stable par intersection finie d'element il faut que

et pour que
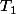
soit stable par reunion quelconque il faut que

.
Maintenant quelle condition doivent avoir A et B? je ne vois pas
2) pour les compacts, on se trouve dans

donc les compacts sont les fermés bornés.
pour le A, on a


et


et

donc

donc je peux dire que A est borné puisque

est contenant dans une partie bornéé.
si je pose
 = x^2+y^4)

est une application continue car c'est une fonction polynome donc continue sur son ensemble de definition qui

et on constate que
 = A)
pour la topologie usuelle {1} est un fermé donc

est fermé car c'est l'image reciproque d'un fermé par une application continue.

est donc compact.
pour le B en eutilisant le meme raisonnement on aura

donc B n'est bornéé donc non compact
pour le C, on a:
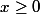
ce qui implique

donc on a
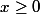
et



n'est donc pas bornéé.
pour le D:
on a
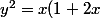)
en developpent et en utilisant la forme canonique on aura
^2-2y^2=1)
là je ne sais pas comment traduire ca. besoin de piste

