Topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 05 Aoû 2014, 22:27
par barbu23 » 05 Aoû 2014, 22:27
Bonsoir à tous,
Pourquoi tout ensemble

muni de la topologie grossière est un espace séparable ?.
Merci d'avance. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Aoû 2014, 00:12
par barbu23 » 06 Aoû 2014, 00:12
Parce que,

, car :

est fermé, non ?
Merci d'avance. :happy3:
-
Trident
- Membre Relatif
- Messages: 410
- Enregistré le: 18 Sep 2010, 15:03
-
 par Trident » 06 Aoû 2014, 03:27
par Trident » 06 Aoû 2014, 03:27
Nan car E n'est pas forcément dénombrable. Si E est non vide, prenons l'ensemble X={x} avec x dans E. L'adhérence de X est un fermé donc c'est soit X ou le vide. C'est pas le vide car X est non vide donc adherence(X)=E donc X est dense dans E. Et il est fini donc au plus dénombrable.
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 07 Aoû 2014, 22:37
par El_Gato » 07 Aoû 2014, 22:37
Salut,
Parcequ'un espace est séparable quand, étant donné deux points x et y distincts de cet espace, tu peux trouver deux ouverts X et Y auxquels x et y appartiennent respectivement, et tels que
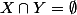
.
Or dans le cas de la topologie discrète il suffit de prendre

et

qui sont ouverts par définition de la topologie discrète, et disjoints si
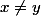
.
barbu23 a écrit:Bonsoir à tous,
Pourquoi tout ensemble

muni de la topologie grossière est un espace séparable ?.
Merci d'avance. :happy3:
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 08 Aoû 2014, 00:23
par jlb » 08 Aoû 2014, 00:23
El_Gato a écrit:Salut,
Parcequ'un espace est séparable quand, étant donné deux points x et y distincts de cet espace, tu peux trouver deux ouverts X et Y auxquels x et y appartiennent respectivement, et tels que
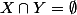
.
Or dans le cas de la topologie discrète il suffit de prendre

et

qui sont ouverts par définition de la topologie discrète, et disjoints si
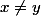
.
euh, petite confusion séparé, séparable?
-
Groucho
- Membre Naturel
- Messages: 67
- Enregistré le: 14 Mai 2014, 13:19
-
 par Groucho » 08 Aoû 2014, 12:49
par Groucho » 08 Aoû 2014, 12:49
Ne pas confondre
espaces séparés : étant donné 2 points (distincts), ils possèdent des voisinages disjoints et
espaces séparables ils possèdent un sous ensemble au plus dénombrable dense (dont l'adhérence est l'espace tout entier).
Si E est muni de la topologie grossière (et est non vide), l'adhérence d'un de ses points quelconque est l'espace tout entier et il est donc séparable.
Si E est vide, la question ne me paraît pas très intéressante, mais on peut dire aussi que l'ensemble vide est dense dans E.
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 13 Aoû 2014, 00:18
par El_Gato » 13 Aoû 2014, 00:18
Ah oui oups pardon, erreur de ma part.
jlb a écrit:euh, petite confusion séparé, séparable?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
muni de la topologie grossière est un espace séparable ?.
.
et
qui sont ouverts par définition de la topologie discrète, et disjoints si
.