Topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Terence00
- Membre Naturel
- Messages: 23
- Enregistré le: 15 Fév 2012, 23:07
-
 par Terence00 » 07 Aoû 2013, 16:47
par Terence00 » 07 Aoû 2013, 16:47
Bonsoir
Quelqu'un pourrait m'aider à faire la démonstration de la prop suivante ?
Soit (E,d) un espace métrique, A une partie de E, x

E. L'ensemble A est borné ssi
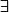
r>0 A
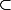
B(x,r)
B(x,r) etant la boule ouverte de centre x et de rayon r
Merci d'avance
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 07 Aoû 2013, 17:10
par L.A. » 07 Aoû 2013, 17:10
Bonjour.
Par définition, ta partie A est bornée donc tu peux l'inclure dans un certaine boule de centre y et de rayon r'. Mais ici, on te demande de prouver que tu peux l'inclure dans une boule (de rayon r) dont le centre x a été fixé au départ dans l'e.m. E.
Quelle relation entre x,y,r et r' assurerait que A est incluse dans B(x,r) ? Pour t'aider tu peux bien sûr faire un dessin.
-
Terence00
- Membre Naturel
- Messages: 23
- Enregistré le: 15 Fév 2012, 23:07
-
 par Terence00 » 07 Aoû 2013, 17:21
par Terence00 » 07 Aoû 2013, 17:21
Merci pour la réponse mais pourriez-vous m'expliquer pourquoi toute partie bornée est incluse dans une boule.
desolé, je suis debutant en matiere de topologie.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 07 Aoû 2013, 17:42
par adrien69 » 07 Aoû 2013, 17:42
Quelle est la définition d'une partie bornée ? Et surtout, quel est son dessin ?
-
Terence00
- Membre Naturel
- Messages: 23
- Enregistré le: 15 Fév 2012, 23:07
-
 par Terence00 » 08 Aoû 2013, 04:03
par Terence00 » 08 Aoû 2013, 04:03
On dit qu'une partie est bornée si elle est incluse dans une boule ouverte ou fermée (dans un espace metrique)
J'ai pas trouvé des infos a propos de son dessin.
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 08 Aoû 2013, 04:47
par ffpower » 08 Aoû 2013, 04:47
Terence00 a écrit:pourriez-vous m'expliquer pourquoi toute partie bornée est incluse dans une boule.
Terence00 a écrit:On dit qu'une partie est bornée si elle est incluse dans une boule ouverte ou fermée
:we:
allongeur de message fait maison
-
ProGramER
- Messages: 1
- Enregistré le: 21 Juil 2013, 23:52
-
 par ProGramER » 08 Aoû 2013, 05:33
par ProGramER » 08 Aoû 2013, 05:33
Terence00 a écrit:Merci pour la réponse mais pourriez-vous m'expliquer pourquoi toute partie bornée est incluse dans une boule.
desolé, je suis debutant en matiere de topologie.
Une partie A de (E,d) est dite bornée ssi pour tout x dans A , d(O,x) 0 ;;
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 08 Aoû 2013, 11:27
par adrien69 » 08 Aoû 2013, 11:27
Terence0 a écrit:J'ai pas trouvé des infos a propos de son dessin.
C'est une blague ?
Ma question n'est pas moqueuse. Je demande honnêtement si c'est une blague.
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 08 Aoû 2013, 16:48
par L.A. » 08 Aoû 2013, 16:48
La définition de ProGramER (qui au passage est ambigue au niveau des quantificateurs) me semble plutôt être la conclusion de l'exercice, c'est vrai que c'est aussi une définition possible mais ce n'est pas le but ici je pense...
Pour Terence00 : calme-toi, souffle un bon coup, et dis-nous exactement ce que tu sais et ce que tu fais ou envisages pour résoudre l'exercice.
Pour le dessin, on ne te parle pas d'un truc précis, juste un petit schéma pour fixer les idées, un moyen de "visualiser" le problème dans le plan si tu veux...
-
Terence00
- Membre Naturel
- Messages: 23
- Enregistré le: 15 Fév 2012, 23:07
-
 par Terence00 » 08 Aoû 2013, 17:14
par Terence00 » 08 Aoû 2013, 17:14
Pour L.A. Il ne s'agit pas d'un exercice. Je suis entrain de découvrir le cours de topologie sur les espaces métriques et les evn.
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 08 Aoû 2013, 19:45
par L.A. » 08 Aoû 2013, 19:45
Exercice, problème, proposition à démontrer, question que tu te poses, c'est pareil.
Bref, ce qu'on aimerait bien savoir, c'est où tu en es. Par exemple, est-ce que tu as suivi l'indication que je t'ai donné au début ?
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 08 Aoû 2013, 19:59
par deltab » 08 Aoû 2013, 19:59
Terence00 a écrit:Pour L.A. Il ne s'agit pas d'un exercice. Je suis entrain de découvrir le cours de topologie sur les espaces métriques et les evn.
Je te conseille de laisser tomber les evn et d'étudier uniquement les espaces métriques. tu as sûrement du voir que le plan

muni de la distance dite euclidienne
=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2)
est bien un espace métrique. Le problème est alors: Quelles sont les conditions pour qu'un disque D(A,r) (de centre A et de rayon r) sont contenu dans un disque D(B,R) et ça ce n'est pas difficile à trouver. Essaie de traduire ça en terme de distance. Le cas général va apparaitre de lui-même.
-
Terence00
- Membre Naturel
- Messages: 23
- Enregistré le: 15 Fév 2012, 23:07
-
 par Terence00 » 08 Aoû 2013, 22:05
par Terence00 » 08 Aoû 2013, 22:05
Ok merci tout le monde
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités