Topologie produit
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
saberication
- Membre Naturel
- Messages: 13
- Enregistré le: 30 Sep 2012, 23:33
-
 par saberication » 06 Oct 2012, 21:41
par saberication » 06 Oct 2012, 21:41
bonsoir a tous ; dans un espace topologique produit ,un produit infini d ouvert n 'est pas nécecerement un ouvert pour la topologie produit ;je sais pas pourquoi?? par contre unproduit fini d ouvert est un ouvert; car c ' est un ouvert élémentaire , aider moi svp :hein:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 06 Oct 2012, 21:54
par Nightmare » 06 Oct 2012, 21:54
Hello,
que penses-tu de

dans
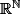
?
-
saberication
- Membre Naturel
- Messages: 13
- Enregistré le: 30 Sep 2012, 23:33
-
 par saberication » 06 Oct 2012, 22:33
par saberication » 06 Oct 2012, 22:33
pardon j 'ai pas compris votre question
-
saberication
- Membre Naturel
- Messages: 13
- Enregistré le: 30 Sep 2012, 23:33
-
 par saberication » 06 Oct 2012, 22:42
par saberication » 06 Oct 2012, 22:42
oui oui si je montre cet ensemble n 'est pas un ouvert de R(n) pour la topologie produit , mon probléme est résolus
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 23:04
par barbu23 » 06 Oct 2012, 23:04
Pourquoi c'est pas un ouvert ? parce que c'est l'intersection quelconque ( dénombrable ) d'ouverts de type

, non ?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 06 Oct 2012, 23:07
par girdav » 06 Oct 2012, 23:07
barbu23 a écrit:Pourquoi c'est pas un ouvert ? parce que c'est l'intersection quelconque ( dénombrable ) d'ouverts de type

, non ?
Pourquoi est-ce qu'une intersection dénombrable d'ouverts serait-elle encore un ouvert ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 06 Oct 2012, 23:08
par barbu23 » 06 Oct 2012, 23:08
girdav a écrit:Pourquoi est-ce qu'une intersection dénombrable d'ouverts serait-elle encore un ouvert ?
C'est pour cette raison que ce n'est pas un ouvert ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Oct 2012, 13:11
par Nightmare » 07 Oct 2012, 13:11
Rappel : La topologie produit sur (Xi,Ti) est la topologie dont les ouverts sont des produits d'ouverts Ui qui sont égaux à Xi sauf pour un nombre fini d'indices i.
En particulier, un ouvert de R^N est un produit cartésien qui contient au moins une fois R. Est-ce le cas de ]0;1[^N ?
-
saberication
- Membre Naturel
- Messages: 13
- Enregistré le: 30 Sep 2012, 23:33
-
 par saberication » 07 Oct 2012, 22:32
par saberication » 07 Oct 2012, 22:32
donc est ce que peut dir un produit infini d 'ouvert n' est pas nécecerement un ouvert pour la topologie produit car il ne contient aucun ouvert élementaire?
-
saberication
- Membre Naturel
- Messages: 13
- Enregistré le: 30 Sep 2012, 23:33
-
 par saberication » 07 Oct 2012, 22:55
par saberication » 07 Oct 2012, 22:55
:)oui Nightmare ; je suis d ' accord avec toi , Merci beaucoup pour la réponse .cordailement .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
