Topologie L3 point fixe dans un compact

[Gurvan44]

Bonjour,
Je suis bloqué dans un exo de pt fixe dans un compact,
Voici le sujet : c’est l’ex 2

https://drive.google.com/file/d/13m4_Ap ... sp=sharing

Et voici ce que j’ai fait, il y a deux choses qui me dérangent pour le moment ( cf « A » et « B »)
https://photos.app.goo.gl/8knnyLQqQepzJFUB9

Merci bcp pour votre attention et bon dimanche

[Ben314]

Salut,
J'ai pas accès à l'énoncé . . .

[Gurvan44]

lien modifié ! dsl

[Ben314]

Pour le A), c'est con comme la lune : le fait que la norme du vecteur tende vers le réel 0 signifie (par définition) que le vecteur tend vers le vecteur nul.
Ensuite tu applique le résultat classique sur les somme de suites dans un e.v.n. pour dire que, vu que et que , c'est que la somme des deux, à savoir , tend vers .

[Ben314]

Pour le B), ça me semble mal barré en procédant de la sorte, surtout qu'à priori, rien ne prouve que les points fixes de f sont forcément à chercher parmi les valeurs d'adhérences de la suite (x_n) : le fait que la suite ait au moins une valeur d'adhérence (car K est compact) prouve qu'il y a au moins un point fixe, mais c'est pas la bonne approche pour montrer que c'est le seul.
Bref, le plus simple et de loin, c'est de partir de zéro (donc de ne pas utiliser la suite (x_n)) et de supposer simplement qu'on a deux point fixes alpha et beta.
Que peut on écrire les concernant ?

P.S. : en regardant de plus prés, je viens de voir qu'il y une erreur dans l'énoné : la définition d'une application contractante, c'est impossible que ce soit exactement celle donnée par l'énoncé. Tu devrais t'en rendre compte justement en répondant à la question (3) sur l'unicité du point fixe.

[Gurvan44]

Super j’ai tout compris merci oui en effet c’est une astuce que j’avais oublié content de la retrouver.
Oui en prenant alpha bêta on trouve alpha - bêta <= k alpha - bêta (en norme) et on déduit k = 0.
L’erreur dans l’énoncé est le < stricte on est d’accord ? Sinon on a une norme qui peut être <0

Merci bien !

[Gurvan44]

Je galère pour la question ii) 1) et la ii)3

Des indications ? ^^

https://photos.app.goo.gl/J3mrVtT7y1H4ahGN8

[Ben314]

L’erreur dans l’énoncé est le < stricte on est d’accord ? Sinon on a une norme qui peut être <0

Oui, c'est plus ou moins ça : la définition de "contractante" ne peut pas être celle donnée dans l'exo. vu que, lorsqu'on prend y=x , ||f(x)-f(x)|| est nul et n'est pas strictement plus petit que k||x-x|| qui lui aussi est nul. Donc avec cette définition là, il n'existerais aucune application contractante (sauf si le compact K est vide).
Et pour que la définition devienne correcte, on peut effectivement mettre une inégalité large à la place de la stricte, ou alors (et c'est plutôt ça que j'aurais fait), préciser que l'inégalité stricte doit avoir lieu pour tout x, y distincts de K.

[Ben314]

Pour le ii)1) c'est évident à condition d'être familier avec la notion de convexité et ce qui va avec :
Pour tout le vecteur est de la forme avec 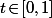donc il est situé sur le segment joignant à (c'est la définition d'un "segment" dans un e.v.n) or et sont tout les deux dans qui est supposé convexe donc le segment qui les joint est contenu dans .
Après, c'est assez évident que l'application en question est contractante (de rapport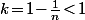 ) donc la question i) te vend qu'elle admet un point fixe.

Le 2) c'est O.K. pour ta prose.

Pour le 3), une fois qu'on la connait, la réponse est triviale : NON, il n'y a en général pas unicité et, pour le démontrer, il suffit de donner un exemple.
Quelle est la fonction le plus simple possible (et de loin...) de K dans K telle que ||f(x)-f(y)|| soit inférieur ou égal à ||x-y|| pour tout x,y de K ?

Sinon, personnellement, j'aurais rajouté une 3em question iii) où l'hypothèse serait que ||f(x)-f(y)||<||x-y|| (strict) pour tout x,y distincts de K : existence de point(s) fixe(s) ? unicité ?

[Gurvan44]

Ok merci bcp Ben ! Je pense que j’ai ce qu’il me faut mnt.
Bonne soirée