Topologie: homéomorphismes

par **legeniedesalpages** » 25 Aoû 2007, 14:18

Bonjour, je suis tombé sur un exo de topo où je n'arrive pas à démarrer:

Soient

et

deux sous-ensembles dénombrables et partout denses de

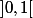
(muni de la topologie induite de

).

a) Montrer qu'il existe une infinité de bijections croissantes de

sur

.

b) Montrer qu'une telle bijection se prolonge d'une façon et d'une seule en un homéomorphisme de

sur lui-meme.

Merci pour votre aide.

EDIT: en fait pour la a), je ne vois meme pas comment montrer qu'il en existe au moins une.

par **aviateurpilot** » 26 Aoû 2007, 02:33

a)
puisque

et

sont dnombrable
on peux ecrire

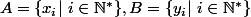
pour

on construit une bijection

tel que

et

donc on a bien une infinite de bijection de A sur B

b) là c'est pas de mon niveau, j'ai meme pas compris c'est quoi "homéomorphisme". lol

par **cesar** » 26 Aoû 2007, 07:09

aviateurpilot a écrit:b) là c'est pas de mon niveau, j'ai meme pas compris c'est quoi "homéomorphisme". lol

c'est une bijection continue, dont la réciproque est continue. ça sert pour dire que deux espaces topologiques sont « les mêmes», mais vus différemment.

par **yos** » 26 Aoû 2007, 11:11

Et " CROISSANTE " tu sais ce que ça veut dire aviateurpilote???

par **kazeriahm** » 26 Aoû 2007, 12:05

attends mais dénombrable ca veut dire "en bijection avec une partie de N" non ?

enfin si c'est bien ca c'est faux ton raisonnement aviateur. Il faut utiliser le fait que A et B sont partout denses

par **legeniedesalpages** » 26 Aoû 2007, 14:29

bonjour,

oui un ensemble est dénombrable si il est en bijection avec N.
Après, je ne vois pas comment exhiber une telle bijection en fonction de A et B.

par **kazeriahm** » 26 Aoû 2007, 14:35

en bijection avec N ou avecv une partie de N ?

par exemple {0,1} est dénombrable ?

par **quinto** » 26 Aoû 2007, 14:46

Dénombrable = en bijection avec N.
Les ensembles finis ne sont pas dénombrables au sens usuel.

par **sandrine_guillerme** » 26 Aoû 2007, 15:39

quinto a écrit:Dénombrable = en bijection avec N.
Les ensembles finis ne sont pas dénombrables au sens usuel.

Bonjour à tous,

en relation avec la dénombrabilité, quelqu'un pourrait m'expliquer le théorème de Cantor, (pour tout ensemble E, les ensembles

et

ne sont pas équipotents) et pourquoi on a pas

avec

signifiant qu'il existe une injection de

à E ..

Merci .

par **tize** » 26 Aoû 2007, 15:51

sandrine_guillerme a écrit:Bonjour à tous,

en relation avec la dénombrabilité, quelqu'un pourrait m'expliquer le théorème de Cantor, (pour tout ensemble E, les ensembles et ne sont pas équipotents) et pourquoi on a pas avec signifiant qu'il existe une injection de à E ..

Merci .

Bonjour Sandrine,
tu devrais peut être ouvrir un nouveau fil...sinon considère que

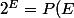et une bijection entre E et P(E), ensuite il faut essayer de faire ressortir une contradiction...

par **sandrine_guillerme** » 26 Aoû 2007, 16:44

tize a écrit:Bonjour Sandrine,
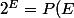tu devrais peut être ouvrir un nouveau fil...sinon considère que et une bijection entre E et P(E), ensuite il faut essayer de faire ressortir une contradiction...

Merci José,

et je demande pardon à legeniedesalpages d'avoir squaté son fil..

par **legeniedesalpages** » 26 Aoû 2007, 18:37

c'est pas bien grave.

tu peux chercher plus simplement par l'absurde qu'il n y a pas de surjection de E dans P(E) ou qu il n y a pas d'injection de P(E) dans E. Je crois qu'il y a une démo sur l article du wiki.

a plus

par **sandrine_guillerme** » 26 Aoû 2007, 19:24

legeniedesalpages a écrit:c'est pas bien grave.

tu peux chercher plus simplement par l'absurde qu'il n y a pas de surjection de E dans P(E) ou qu il n y a pas d'injection de P(E) dans E. Je crois qu'il y a une démo sur l article du wiki.

a plus

Oui C'est bon, c'est fait !

Merci encore ... :lol4:

par **legeniedesalpages** » 27 Aoû 2007, 10:55

pour la a), dois-je utiliser le fait que tout point de A est limite d'une suite de points de B (ou le contraire) ? Le fait que les bijections doivent etre croissantes ne facilite pas la tache.

par **yos** » 27 Aoû 2007, 12:53

Toute la difficulté est bien d'avoir une bijection croissante. S'il y en a une (qu'on note f), il y en a une infinité par le procédé suivant :
on fixe a dans A, b dans B, on prend une bijection croissante u de ]0,a[ dans
]0,b[, on pose g(a)=b et on complète avec une bijection croissante v de ]a,1[ sur ]b,1[. L'existence de u et de v ne pose pas plus de problème que celle de f. La bijection g obtenue est bien croissante et on peut faire ça avec n'importe quel a de A ou b de B, d'où l'infinité recherchée.
Mais le problème est l'existence d'une bijection croissante f. Je suis pas sûr qu'on puisse en exhiber une (i.e. la construire). Avec l'axiome du choix, on peut fabriquer une injection croissante je pense.

Peux-tu me préciser le niveau de l'exercice, la source, le contexte? Merci.

par **Yipee** » 27 Aoû 2007, 13:36

Je dirais (mais je ne suis pas sur) que l'on doit pouvoir utiliser Zorn. En effet l'ensemble

est inductif (c'est là que je n'ai pas bien vérifié). Dès lors il admet un élément maximal. Cet élément ne peut-être que (A,B).

par **yos** » 27 Aoû 2007, 14:20

A creuser mais prouver l'inductivité avec Y,Y' et Z,Z' dénombrables me semble aussi dur que la question de départ.

On peut peut-être faire ceci avec ton idée :

soit

une bijection de

sur A et

une bijection de

sur B.

Pour n fixé, on prend

et

une bijection croissante de

sur

.
Il est clair qu'on peut construire les

par récurrence de façon que la restriction de

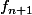
à

soit

.
Bref je travaille avec un ensemble plus petit qui, lui, est clairement inductif.

par **Yipee** » 27 Aoû 2007, 14:33

Cela ne me semble pas si dur que cela de montrer que c'est inductif. Soit

une partie totalement ordonnée. Alors on peut définir l'élément

.
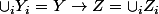
Cette application est bijective et croissante.

par **yos** » 27 Aoû 2007, 16:07

Je crois pas : essaie avec deux éléments Y, Y' dénombrables (infinis) et Z, Z'.
Tu as une application croissante

et une autre

. Comment définis-tu l'application de

dans

pour que la croissance soit préservée?

par **legeniedesalpages** » 27 Aoû 2007, 16:26

Bonjour, merci deja pour vos indications, je vais suivre vos pistes et decouvrir au passage ce lemme de zorn.

"Peux-tu me préciser le niveau de l'exercice, la source, le contexte? Merci."
c'est un exercice dans le contexte de la topologie de la droite reelle, d'un debut de cours de topologie.
la source: "Cours de topologie", Gustave Choquet ed. Dunod.
niveau debut L3 je pense.

Topologie: homéomorphismes

topologie: homéomorphismes

Qui est en ligne