Salut à tous, j'ai un peu du mal à comprendre quelque chose à propos de la topologie *faible. Soit E un espace vectoriel normé. On note
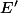
son dual, c'est à dire l'ensemble des formes linéaires continues sur E. On rappelle que la topologie *faible est la topologie la moins fine (i.e. celle qui contient le strict minimum d'ouverts) rendant continue les applications
)
où x parcourt E.
Il s'agit donc de la topologie engendrée par
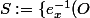, x \in E, O \ \text{ouvert de} \ \mathbf{R}\})
. On note
)
cette topologie.
Tout ouvert de
))
s'écrit donc comme réunion d'intersections finies d'éléments de S.
Première question : Puisque tout ouvert

de
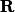
s'écrit comme réunion d'intervalles ouverts, peut-on dire que
)
est la topologie engendrée par
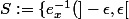, x \in E, \epsilon \in \mathbf{R}\})
?
Seconde question. Il est dit dans une démonstration la chose suivante. Soit

un élément quelconque de
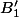
(où
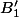
est la boule unité de
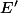
mais je ne pense pas que cela soit important pour ma question). Soit

un ouvert de
))
contenant
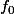
. Alors il est dit et c'est la que je ne comprend pas : il existe un nombre fini

dans E et
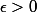
tel que l'ensemble suivant
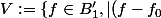(y_j)| 0)
tels que :
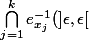 \subseteq O.)
Mais justement :
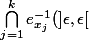 = \{f \in B_1', |f(y_j)| < \epsilon \ \forall j=1,\dots,k \})
Il me manque donc ce "
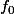
" :mur: Je me doute bien qu'il vient du fait que

mais je n'arrive pas à le montrer.
Merci.