Topologie - Espace produit

[Stringer]

Petite question de topologie, plus précisément sur les produits d'espaces topologiques.

Dans mon cours on commence par définir la topologie suivante dans le cas d'un produit de deux espaces ExF:

O = { l'ensemble des réunions d'ouverts élémentaires UxV, ou U est un ouvert de E et V est un ouvert de F }

Donc ça il faut bien sur démontrer que ça définit bien une topologie ...

Maintenant par récurrence, ils nous définissent quelques chose d'analogue pour un produit de n espaces topologiques.

Ma question est: pourquoi ne pas généraliser aux produits d'un nombre infini d'espace ?

Les propriétés restent bien les mêmes non ? ( Je pense en particulier aux trucs du genre : l'adhérence du produit est le produit des adhérences, l'intérieur du produit est le produit des intérieurs... )

Si c'est faux, vous avez un contre exemple ?

merci :we:

[arnaud32]

pour un produit infini d'especes topologiques, les ouverts elementatires sont les produits di la forme
ou les 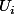sont des ouverts de et 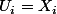sauf pour un nombre fini d'indices

http://fr.wikipedia.org/wiki/Topologie_produit

[Stringer]

pour un produit infini d'especes topologiques, les ouverts elementatires sont les produits di la forme
ou les sont des ouverts de et sauf pour un nombre fini d'indices

http://fr.wikipedia.org/wiki/Topologie_produit

c'est exactement ce que je comprends pas, pourquoi cette condition supplémentaire ?

Dans le livre avec lequel je travaille, pour démontrer que l'ensemble O définit bien une topologie, ils montrent que l'intersection de deux ouverts élémentaires est un ouvert élémentaire, et de plus ExF est un ouvert élémentaire, donc cela suffit à démontrer que l'ensemble O définit une topologie sur ExF.

Mais la démonstration n'est-elle pas exactement la même dans le cas d'un produit infini ?

si on prends un produits d'espaces Ei, i €I avec I infini :


On peut définir exactement de la même manière un ouvert elementaire :

et si on fait l'intersection de deux ouverts élémentaires :



qui est bien un ouvert élémentaires, vu que l'intersection de deux ouverts de Ei est un ouvert de Ei .



Quelle est la subtilité ? :mur:

[arnaud32]

la topologie produit est la topologie qui rend continue toutes les projections.
De ce fait tu as pour tout i et tout ouvert de , qui est ouvert
quell est la forme de ?

[Nightmare]

Hello,

si l'on considère tous les produits d'ouverts (pas seulement ceux contenant une infinité de Xi), ça ne forme pas une topologie, par contre ça forme une base de topologie, qu'on appelle la "topologie des boîtes" (box topology). Je ne connais pas d'intérêt pratique de cette topologie si ce n'est l'utiliser comme contre-exemples. Ce qui est certain est qu'elle ne répond pas aux besoins de la topologie produit, à savoir obtenir la continuité des projections.