bonjour a tous.
Je me bloque sur une question de topologie qui a l'air plutot facile mais je n'arrive pas a repondre. jai essayé plusieurs choses et ca marche pas.
(E,d) est un espace metrique.
On definit d'(x,y)=d(x,y)/(1+d(x,y))
il faut montrer que d' est une distance sur E.
je n'arrive pas a demontrer l'inegalité triangulaire pour d'.
merci
Topologie, distances
4 messages
- Page 1 sur 1
Re: topologie, distances
Bonjour,
On aimerait montrer que :
pour tous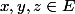
\le d'(x,y)+d'(y,z))
Si on explicite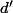 , on aimerait donc avoir :
, on aimerait donc avoir :
}{1+d(x,z)} \le \frac{d(x,y)}{1+d(x,y)} + \frac{d(y,z)}{1+d(y,z)})
c'est-à-dire :
}{1+d(x,z)} \le \frac{d(x,y)+d(y,z)+2d(x,y)d(y,z)}{1+d(x,y)+d(y,z)+d(x,y)d(y,z)})
Autrement dit, on aimerait avoir :
(1+d(x,y)+d(y,z)+d(x,y)d(y,z)) \le (1+d(x,z))\big (d(x,y)+d(y,z)+2d(x,y)d(y,z)))
Tout ce qu'il reste à faire est de vérifier qu'on a bien cette inégalité, tout en se rappelant que \le d(x,y) + d(y,z))
On aimerait montrer que :
pour tous
Si on explicite
c'est-à-dire :
Autrement dit, on aimerait avoir :
Tout ce qu'il reste à faire est de vérifier qu'on a bien cette inégalité, tout en se rappelant que
Re: topologie, distances
merci bcp. c'est en fait ca ce que j'ai fait mais je me suis arreté a la longue inegalité en croyant que je ne vais jamais aboutir au resultat demandé. il fallait donc juste faire un petit effort.
Re: topologie, distances
Salut,
On peut effectivement se lancer dans des calculs pourris ou bien . . . prendre un peu de recul . . .
Ta distance d' elle s'écrit f(d) où f est la fonction x->x/(x+1).
Et pour montrer l'inégalité triangulaire pour d', sachant qu'elle est vraie pour d, il suffit de montrer que, si a<=b+c (réels positifs) alors f(a)<=f(b)+f (c).
Comme f est croissante, a<=b+c implique f(a)<=f (b+c) donc il suffit de montrer que f(b+c)<=f(b)+f(c).
Or f(b+c)-f (b)=c.f'(u) avec u entre b et b+c et f(c)=f(c)-f(0)=c.f'(v) avec v entre 0 et c donc, modulo d'avoir pris c<b pour garantir que v<u, le résultat découle de la décroissance de f'.
On peut effectivement se lancer dans des calculs pourris ou bien . . . prendre un peu de recul . . .
Ta distance d' elle s'écrit f(d) où f est la fonction x->x/(x+1).
Et pour montrer l'inégalité triangulaire pour d', sachant qu'elle est vraie pour d, il suffit de montrer que, si a<=b+c (réels positifs) alors f(a)<=f(b)+f (c).
Comme f est croissante, a<=b+c implique f(a)<=f (b+c) donc il suffit de montrer que f(b+c)<=f(b)+f(c).
Or f(b+c)-f (b)=c.f'(u) avec u entre b et b+c et f(c)=f(c)-f(0)=c.f'(v) avec v entre 0 et c donc, modulo d'avoir pris c<b pour garantir que v<u, le résultat découle de la décroissance de f'.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
