Topologie : dessin
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mounch1810
- Membre Naturel
- Messages: 23
- Enregistré le: 31 Jan 2015, 14:40
-
 par mounch1810 » 22 Fév 2015, 18:50
par mounch1810 » 22 Fév 2015, 18:50
Bonjour voici mon problème:
J'ai un compact
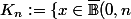\ :\ \delta_\Omega(x)\geq \frac{1}{n}\})
Nous travaillons avec la norme euclidienne sur
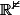
et
 = \inf_{y\in \mathbb{R^2}-\Omega} \left\|x-y\right\|)
Mon ensemble
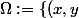\in\mathbb{R^2}\ :\ x^2+y^2<1\})
est le disque unité dans
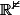
Je dois donner l'expression de

et dessiner

L'expression de

mais je ne vois pas comment aller plus loin et donc impossible de dessiner.
Merci de votre aide
-
mathelot
 par mathelot » 22 Fév 2015, 19:42
par mathelot » 22 Fév 2015, 19:42
Les
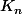
sont des couronnes
-
mounch1810
- Membre Naturel
- Messages: 23
- Enregistré le: 31 Jan 2015, 14:40
-
 par mounch1810 » 22 Fév 2015, 21:11
par mounch1810 » 22 Fév 2015, 21:11
mathelot a écrit:Les
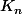
sont des couronnes
Donc entre la boule de centre 0 et de rayon n et ???
-
mathelot
 par mathelot » 23 Fév 2015, 08:25
par mathelot » 23 Fév 2015, 08:25
Dans
)
et pas dans B(0,1+1/n)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités