Topologie dans Rn...

[benj3850]

hello tout le monde.
j'ai une petite question sur laquelle je bloque :
soit E l'ensemble des (x,y) tels que y<= x+3 et y>=x^2 +1
il faut dire si c'est ensemble est fermé, ouvert, borné compact ?
j'ai dit (corrigez moi si je me trompe ;) ) qu'il etait fermé en prenant une suite (xn, yn) telle que l=(a,b) soit sa limite, donc xn->a et yn->b, donc on a a+3>=b et b>=a^2 +1 donc l appartient a E donc E est fermé.
par contre ensuite c'est la ou je bloque car je dirait que ce n'est pas un ensemble borné et donc non compact, qu'en pensez vous ?
merki de vos réponses

ps : comment montre t on que si A est ouvert alors A+B est ouvert sachant que A et B non vides et appartenant à E un espace vectoriel ?

[jose_latino]

Par exemple, tu as que , donc , ça veut dire que , alors on peut trouver que la composante est bornée aussi. Bon courage! :zen:

[benj3850]

ah ouai j'avais pas vu ca comme ca lol
merci bien pour ta reponse jose :)

[Zebulon]

Bonsoir,
pour le P.S., soit , alors il existe et tels que .
A est ouvert donc il existe tel que
B est ouvert donc il existe tel que
il s'agit de déterminer un ouvert W de E tel que .

[jose_latino]

ps : comment montre t on que si A est ouvert alors A+B est ouvert sachant que A et B non vides et appartenant à E un espace vectoriel ?

Tu veux dire A et B sont inclus dans E.

[benj3850]

Tu veux dire A et B sont inclus dans E.

oui A et B sont deux parties non vides de E

[benj3850]

à la suite de la question il y a : indication : commencer par le cas où B est réduit à un point.

[yos]

Si B est réduit à un point, A+B est un translaté de l'ouvert A donc A+B est ouvert.
Dans le cas général, A+B est la réunion des ouverts A+b avec b dans B.

[benj3850]

J'ai une autre petite question :

Soient Rn muni d'une distance d, A une partie non vide de Rn et x appartenant à Rn. On définit la distance de x à A comme étant le réel défini par :

d(x,A) = Inf d(x,y) y appartenant à A

il faut alors montrer que d(x,A) = 0 équivaut à x adhérent à A.


Voila ce que j'ai fait :

J'ai déja dit que d(x,A) existe car d(x,y) est minoré par 0 et A non vide.
Ensuite :
d(x,A) = 0 équivaut à Inf d(x,y) = 0, ce qui équivaut à d(x,y) = 0.
On obtient alors que :
pour tout epsilon (e) > 0, il existe y appartenant à A tel que d(x,y) < e
équivalant à 0 <= d(x,y) < e équivalant à :
d(x,A) <= d(x,y) < e + d(x,A) car d(x,A) = 0
Donc x adhérent à A.

Pourriez-vous me dire si ce que j'ai écrit comporte des erreurs, notamment dans les équivalences, et si ce qui était à démontrer l'est.

merci beaucoup pour vos réponses

[Zebulon]

Bonsoir,

d(x,A) = Inf d(x,y) y appartenant à A

il faut alors montrer que d(x,A) = 0 équivaut à x adhérent à A.


Voila ce que j'ai fait :

J'ai déja dit que d(x,A) existe car d(x,y) est minoré par 0 et A non vide.
Ensuite :
d(x,A) = 0 équivaut à Inf d(x,y) = 0, ce qui équivaut à d(x,y) = 0.

Non, pourquoi? L'inf n'est pas forcément atteint. D'ailleurs, il est atteint si et seulement si x appartient à A.

[quote]On obtient alors que :
pour tout epsilon (e) > 0, il existe y appartenant à A tel que 0 0\ \exists a\in A\ 0\leq d(x,a) 0\ \exists a\in A\ 0\leq d(x,a)0\ \exists a\in A\ a\in\mathcal{B}(x,r)[/TEX].

[benj3850]

daccor, merci bien pour ton explication Zébulon :)

[Zebulon]

Je vous en prie. A bientôt ! :we:

[nimiclius]

- Si d(x,a)=0 alors inf d(x,y)=0
alors il edxiste y ds A tq d(x,y)=0
alors il existe y ds A tq x=y (def de la distance)
par suite x adhérent a A

-Si x adhérent à A
(on sait que d(x,y) >= 0 donc inf d(x,y) >=0)
alors inf d(x,y)=0 en prenant y=x

TOUT SIMPLEMENT

[Zebulon]

- Si d(x,a)=0 alors inf d(x,y)=0
alors il edxiste y ds A tq d(x,y)=0

Non ! Ca, ça veut dire que l'inf est atteint ce qui n'a pas de raison d'être vrai.

[BQss]

hello tout le monde.
j'ai une petite question sur laquelle je bloque :
soit E l'ensemble des (x,y) tels que y=x^2 +1
il faut dire si c'est ensemble est fermé, ouvert, borné compact ?
j'ai dit (corrigez moi si je me trompe ) qu'il etait fermé en prenant une suite (xn, yn) telle que l=(a,b) soit sa limite, donc xn->a et yn->b, donc on a a+3>=b et b>=a^2 +1 donc l appartient a E donc E est fermé.
par contre ensuite c'est la ou je bloque car je dirait que ce n'est pas un ensemble borné et donc non compact, qu'en pensez vous ?
merki de vos réponses

ps : comment montre t on que si A est ouvert alors A+B est ouvert sachant que A et B non vides et appartenant à E un espace vectoriel ?

LOL, les gars je vous propose une reponse mi analytique:

Dites moi personne n'a eu l'idée de les tracer ces deux graphes tout naz...

C'est evidemment ni un ouvert ni un fermé mais borné... Et donc non compact car tout les compacts de R^n sont fermés bornés... Par contre il est convexe, connexe et tout le tralala lol.


L'ensemble equivaut à l'intersection de:
(x;"y=x^2+1") c'est a dire un fermé non bornée de R^2

]-1;2[x[x^2+1;x+3[, c'est a dire une reunion d'ensemble non denombrable...


Maintenant vous allez me dire comment je montre que c'est ce petit bout de R^2 entre ces deux courbes.
Et bien trivial, vous etudiez juste les variations de ces deux courbe en x et prouver qu'elle se coupent en x=-1 pour ne plus jamais se rencontrer(croissance opposées), pareille pour 1, x^2+1 rencontre x+3 et sa dérivée est alors constamment superieur a 1 et donc y est alors au dessus de x+3.
Evidemment comme les deux fonctions en x sont continues, le domaine entre ces deux graphes est bien définie...

On en deduit aisement que y=x^2+1 sur ]-1;2[ exclu(exclu car en ces points la y=x+3 evidemment).

Donc apres etude des fonction en x, on en deduit que notre ensemble est non fermé(ca c'est trivial), rien que parce que x=-1 et x=2 sont exclu pour tout y alors que pour y=-1 et 2 il constitue la une borne inf trivial en x et y fixé, donc deux elements de l'adhérence qui n'appartiennent pas a l'ensemble...
Et non ouvert en procedant d'une logique similaire en cherchant un element qui appartient a l'adherence et qui appartient a l'ensemble

Plus simplement pour tout x, y<x^2+1 donc x^2+1 qui appartient a l'adhérence mais n'appartient pas a l'ensemble(pour montrer que ce n'est pas un fermé par exemple)...

Pour borné, il est donc borné en x(d'apres l'etude de l'intersection des graphes) et comme y est fonction de x, il est borné en y ....

Pour la convexité, une analyse simple des graphes nous donne une reponse...

[benj3850]

c'est re moi ^^ lol
voici un nouvel exercice sur lequel je travaille :

Soit la fonction f : D inclu à R2 -> R tel que :

f(x,y) = (x + y - 1) / | x + y - 1|

1) Donner le domaine de définition de f :

voici donc ce que j'ai fait (comme d'habitude, s'il y a une erreur ou une façon plus simple, hésitez pas !) :

j'ai simplement dit que D = R2 - {(x,y) appartenant à R2 tels que :
x + y = 1 <=> y = 1 - x}

J'ai ensuite posé pour la suite F = {(x,y) appartenant à R2 tels que :
x + y = 1 <=> y = 1 - x}

donc si vous suivez bien, lol, D = R2 - F

2) Montrer que D est un ouvert de R2 :

Cela revient à montrer que R2 - D est un fermé de R2 cad que F est un fermé de R2 :

Soit (xn,yn) une suite CV d'éléments de F et soit l = (a,b) sa limite.

on a alors : xn -> a et yn -> b

=> 1 - a = b

donc (a,b) appartient à F donc F est unb fermé de R2 et par conséquent D un ouvert de R2.

3) Montrer que (1,0) est adhérent à D :

la je ne suis pas sur du tout de ce que j'ai fait, je sais pa si on a le droit de faire ça :

soit (1/n + 1, 1/n) une suite d'éléments de D.
f(1/n + 1, 1/n) = 1
et (1/n + 1, 1/n) -> (1,0) donc le point (1,0) est adhérent à D (:$ lol)


4) Soit xn = (1 + ( (-1)^n / n ), 0) pour n entier non nul. Montrer que la suite (f(x2n)n) est convergente ainsi que la suite (f(x2n+1)n.Conclure

(Je sais pas du tout si c'est ca, (je tente... lol) )
Je dirais que f(x2n) = ... = 1 qui tend vers 1 évidemment donc f(x2n) est convergente ???
de même pour f(x2n+1) = ... = -1 -> -1 donc f(x2n+1).
La conclusion pareil je tente : je dirais que x2n -> (1,0) de même que x2n+1.
On a donc trouvé deux suites de D convergeant toutes les deux vers le point (1,0) mais où f(x2n) = 1 != f(x2n+1) = -1 donc f n'est pas continue au point (1,0) ???

Merci d'avances pour vos commentaires :)

J'oubliais la question 5) (à laquelle je n'ai rien compris !) :
Utiliser des restrictions à des parties de D pour démontrer que f n'a pas de limite en (1,0).

[Zebulon]

Bonsoir,

Soit la fonction f : D inclu à R2 -> R tel que :

f(x,y) = (x + y - 1) / | x + y - 1|
1) Donner le domaine de définition de f :

voici donc ce que j'ai fait (comme d'habitude, s'il y a une erreur ou une façon plus simple, hésitez pas !) :

j'ai simplement dit que D = R2 - {(x,y) appartenant à R2 tels que :
x + y = 1 y = 1 - x}

J'ai ensuite posé pour la suite F = {(x,y) appartenant à R2 tels que :
x + y = 1 y = 1 - x}

donc si vous suivez bien, lol, D = R2 - F

Je suis d'accord pour le domaine de définition de f.

2) Montrer que D est un ouvert de R2 :

Cela revient à montrer que R2 - D est un fermé de R2 cad que F est un fermé de R2 :

Soit (xn,yn) une suite CV d'éléments de F et soit l = (a,b) sa limite.

on a alors : xn -> a et yn -> b

=> 1 - a = b

donc (a,b) appartient à F donc F est unb fermé de R2 et par conséquent D un ouvert de R2.

Je suis d'accord que pour montrer que D est ouvert dans , il suffit de montrer que F est fermé dans . Mais regardez bien comment est défini F. Ne peut-on pas trouver g une application continue et U un fermé de 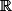tel que ?

[benj3850]

J'ai encore besoin de votre aide ! lol

Je dois étudier la continuité de la fonction :
f : R2 -> R
(x,y) -> { (x + y)²cos(1/x)cos(1/y) si xy != 0
{ 0 si xy = 0


J'ai dit que xy != 0 => x !=0 et y != 0 donc (x + y)²cos(1/x)cos(1/y) est continue sur R² - (0,0) car c'est un produit de plusieurs fonctions continues (je crois que c'est une propriété des limites).

xy = 0 => x=0 ou y=0, ce qui laisse alors plusieurs cas :

*le cas x=0 et y appartenant à R*
*x appartenant à R* et y = 0
*et le cas x=0 et y=0

mais pour chaque cas je n'arrive pas à montrer que c'est continue en 0
auriez vous une solution ?