[L3] Topo, Points isolés

[Doraki]

Soit xQ, x>0
Soit y Q tel que d(x,y) soit minimale et y>x
Q est dense dans R, donc il existe z R tel que :

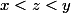
donc

Ainsi je prends

Pourquoi tu as besoin de dire que Q est dense dans R pour montrer qu'il y a un réel entre x et y ?

Si je prends x = 1/3, je comprends pas quel y tu choisis ?

[Doraki]

Dis-moi quel y tu choisis pour x = 1/3.
Est-ce que c'est y = 1/2 ?

[Doraki]

Pourquoi tu ne peux pas l'expliciter ?
Un rationnel c'est une fraction, t'es censé pouvoir l'écrire concrètement.
y = a/b avec a et b entiers. J'te demande juste qui sont a et b.

Est-ce que c'est 10000/29999 ?

[Doraki]

Est-ce que le rationnel qui suit 1/3 c'est 10000/29999 ?
Est-ce que c'est 100000/299999 ?
Est-ce que c'est l'un des environs 3*10^12 rationnels entre 1/3 et 1 dont le dénominateur est < un million ?

Est-ce que si je te posais une infinité de questions du genre "est-ce que c'est a/b ?", où a et b sont des vrais entiers et où je pose la question pour toutes les paires d'entiers avec b non nul, est-ce que, à un moment, tu répondrais oui ?

[Doraki]

Bon j'abandonne.
Ce rationnel n'existe pas.
Tu réponds non à toutes les questions parceque pour tout y rationnel candidat, bah par exemple (1/3 + y)/2 est un rationnel qui est plus proche de 1/3 que y donc y ne peut pas être un "plus petit rationnel plus grand que 1/3".