F"(x) + f(x) = 0

par **barbu23** » 26 Nov 2009, 12:47

Salut à tous : :happy3:
Soit

.
Alors :

est solution de l'équation differentiele linéaire :

Procédons à la resolution de cette équuation :
L'ensemble des solution est evidemment :

Je voudrais savoir pour quelle valeurs de

et de

dans

, on a

, puisque

est aussi une solution de :

Merci d'avance ! :happy3:

par **barbu23** » 26 Nov 2009, 12:53

D'habitude , on écrit :

( Relations trigonometriques )
Mais :

, ce qui contredit l'affirmation du cours que les coefficients doivent être dans

.
MErci de votre aide ! :happy3:

par **Skullkid** » 26 Nov 2009, 13:08

Salut, pourquoi c1 et c2 devraient-ils être réels ?

On peut voir assez facilement qu'il n'existe pas c1 et c2 réels tels que

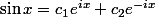
: en évaluant en 0 ça donne c1 + c2 = 0 puis nécessairement c1 = 1 / 2i.

par **legeniedesalpages** » 26 Nov 2009, 13:11

Bonjour,

l'ensemble des solutions réelles de ton équation est

.

barbu23 a écrit:L'ensemble des solution est evidemment :

Non, on peut seulement supposer

.

par **barbu23** » 26 Nov 2009, 18:04

Merci pour ces precisions à vous deux ! :happy3:

par **grikor** » 26 Nov 2009, 18:11

bonjour,
f"+f=0; ff"+ff'=(1/2)*(f'²+f²)'=0, alors f'²+f²=c; df/sqrt(c-f²)=dx

arctg[f/sqrt(c-f²)=x+c...f=sqrtc*sin(x+c)