X
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Mai 2007, 20:00
par mehdi-128 » 26 Mai 2007, 20:00
Bonsoir ,voila un exercice me bloque complètement.
Calculer :
1*2*3+2*3*4+.............+1000*1001*1002
On demande en fait une forme générale puis calculer:
S=sum(p=0..n)((p+1).........(p+k))
merci.....
-
manelle
- Membre Naturel
- Messages: 42
- Enregistré le: 16 Juil 2006, 10:00
-
 par manelle » 26 Mai 2007, 20:32
par manelle » 26 Mai 2007, 20:32
Je te propose de remarquer que :
(p+1)...(p+k) x^p est la dérivée k-ième de x^(p+k)
et essaie de finir , sinon je t'aide un peu plus .
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Mai 2007, 20:45
par mehdi-128 » 26 Mai 2007, 20:45
J'ai une légère idée:
On pose: P(X)=X^(p+k) on obtient: la dérivée k-ième de P en 1 vaut:
(p+1)............(p+k)
Mais ensuite j'ai pas trop d'idée....
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Mai 2007, 21:41
par Joker62 » 26 Mai 2007, 21:41
Le truc c'est que tu connais déjà ce que vaut la somme des x^k pour k allant de 0 à l'infini et pour |x| < 1 ça vaut 1 / (1-x)
Donc Bon après suffit de savoir dériver.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Mai 2007, 22:07
par mehdi-128 » 26 Mai 2007, 22:07
Ah ok je vais essayer merci...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Mai 2007, 22:11
par mehdi-128 » 26 Mai 2007, 22:11
Oui mais je comprends pas un truc:la somme que tu m'a donné vas a l'infini et moi je veux une somme finie....
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 26 Mai 2007, 22:30
par Joker62 » 26 Mai 2007, 22:30
Si tu poses

Et

Alors tu peux faire le rapprochement entre S_n et F_n par la dérivée k ième de Fn
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 26 Mai 2007, 22:52
par mehdi-128 » 26 Mai 2007, 22:52
oui merci mais j'obtiens par dérivation d'un produit:
Fn^(kieme)=sum(k=0..n)(x^k)*p(p-1)......(p-k+1)*x^(p-k) +x^(p)* sum(l=k..n) l(l-1)....(l-k+1)x^(k-l)
c'est ca ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 27 Mai 2007, 10:23
par yos » 27 Mai 2007, 10:23
Pour calculer la somme des k(k+1)(k+2), on peut chercher un polynôme de degré 4 tel que
-P(X)=X(X+1)(X+2))
. La somme cherchée est alors "télescopique".
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Mai 2007, 10:42
par mehdi-128 » 27 Mai 2007, 10:42
En passant a la somme j'obtiens:
P(p+1)-P(0)=sum(k=0..p)( k(k+1)(k+2))
mais ensuite je suis bloqué....Pourquoi le polynome recherché est de degré 4?
-
Rafar
- Membre Naturel
- Messages: 37
- Enregistré le: 19 Mai 2007, 20:47
-
 par Rafar » 27 Mai 2007, 10:51
par Rafar » 27 Mai 2007, 10:51
yos a écrit:Pour calculer la somme des k(k+1)(k+2), on peut chercher un polynôme de degré 4 tel que
-P(X)=X(X+1)(X+2))
. La somme cherchée est alors "télescopique".
J'avais la même idée que Yos.
Si je ne me trompe pas, en posant
 \, = \, X^4+2X^3-X^2-2X)
on a :
 - P(X) \, = \, 4 X(X+1)(X+2))
On a donc :
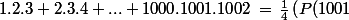 - P(0) \right))
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Mai 2007, 11:04
par mehdi-128 » 27 Mai 2007, 11:04
ok merci .....
-
manelle
- Membre Naturel
- Messages: 42
- Enregistré le: 16 Juil 2006, 10:00
-
 par manelle » 27 Mai 2007, 16:38
par manelle » 27 Mai 2007, 16:38
De mon côté , la méthode générale proposée plus haut n'aboutit pas : la dérivée k-ième se présente très compliquée après l'utilisation de la formule de Leibniz , et la limite en 1 qui existe puisque la fonction est bien C^k en 1 n'est pas simple ...
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 27 Mai 2007, 16:48
par Joker62 » 27 Mai 2007, 16:48

non ?
Enfin à moins que j'ai perdu tout mes souvenirs d'ANA3 :S
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Mai 2007, 16:58
par mehdi-128 » 27 Mai 2007, 16:58
J'ai essayé de calculer la dérivée je vois pas comment t'obtiens cette expression......
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Mai 2007, 17:03
par mehdi-128 » 27 Mai 2007, 17:03
J'obtiens comme dérivée (k-1) ième:
p(p-1)*....*(p-k+2)*x^(p-k+1)+........................+(p+k)*.......*(p+2)*x^(p+1)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 27 Mai 2007, 17:12
par Joker62 » 27 Mai 2007, 17:12
Ah j'dois tout confondre c'est bizarre lol
Purée ça craint :D
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 27 Mai 2007, 17:21
par mehdi-128 » 27 Mai 2007, 17:21
C'est peut-etre moi qui me trompe....Je voulais juste savoir comment t'obtenais cette expression de la dérivée...
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 27 Mai 2007, 17:26
par Joker62 » 27 Mai 2007, 17:26
Non c'est toi qui à raison évidemment !
-
Bouchra
- Membre Relatif
- Messages: 113
- Enregistré le: 13 Juil 2006, 15:38
-
 par Bouchra » 27 Mai 2007, 18:33
par Bouchra » 27 Mai 2007, 18:33
Bonjour,
On a
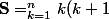\ldots(k+p) = \Bigsum_{k=1}^{n}\Bigprod_{i=0}^{p}<br />(k+i)\\<br /><br />\mathbf{S} = (p+1)! \Bigsum_{k=1}^{n} \frac{k(k+1)\ldots(k+p)}{(p+1)!}<br />\\<br /> \mathbf{S} = (p+1)! \Bigsum_{k=1}^{n} C_{k+p}^{p+1}<br />\\)
Et :

...
:happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 145 invités


 Alors tu peux faire le rapprochement entre S_n et F_n par la dérivée k ième de Fn
Alors tu peux faire le rapprochement entre S_n et F_n par la dérivée k ième de Fn non ?
non ?