Hn
16 messages
- Page 1 sur 1
Hn
Bonsoir,
je me pose une question, je vois que l'on fait souvent une minoration pour montrer que Hn (la série harmonique) diverge, mais est-ce qu'on a le droit de mettre la série de la forme (S c'est la série de 1 à n) (1/n)S(f(k/n)), ce qui donne l'intégrale de 0 à 1 de dx/x, qui diverge.
Ca semblerait à priori plus rapide, reste à savoir si c'est bon.
je me pose une question, je vois que l'on fait souvent une minoration pour montrer que Hn (la série harmonique) diverge, mais est-ce qu'on a le droit de mettre la série de la forme (S c'est la série de 1 à n) (1/n)S(f(k/n)), ce qui donne l'intégrale de 0 à 1 de dx/x, qui diverge.
Ca semblerait à priori plus rapide, reste à savoir si c'est bon.
Modifié en dernier par qaterio le 15 Oct 2018, 21:40, modifié 1 fois.
Re: Hn
Oui c'est ça, mais ça me semble bon, y'a même une formule plus générale (et c'est assez intuitif lorsqu'on a un graphique) mais le truc, c'est que comme dans les livres, je vois pas cette démonstration (et qu'elle me semble assez banale), je m'interroge donc sur sa fiabilité ici...
Je vais reprendre, on a S(1/k)=(1/n)*S(1/(k/n)) qui devrait être égale à l'intégrale de 0 à 1 de dx/x= ln(1)-ln(0+)=+oo.
Je vais reprendre, on a S(1/k)=(1/n)*S(1/(k/n)) qui devrait être égale à l'intégrale de 0 à 1 de dx/x= ln(1)-ln(0+)=+oo.
Modifié en dernier par qaterio le 15 Oct 2018, 21:57, modifié 1 fois.
Re: Hn
C'est que c'est inutile de faire un changement de variable sur l'intégrale de 1 à inf de dx/x, on obtient tout de suite la divergence ...
Re: Hn
Oh, y'a eu un quiproquo (bon en même temps j'utilise pas Latex, c'est pas la première fois qu'on me le reproche, un jour j'apprendrai à utiliser sérieusement Latex), je parlais de la somme des 1/k de k=1 à n. Et de sa limite quand n tend vers +oo.
Re: Hn
Salut,
Le problème, c'est de savoir quel théorème tu compte utiliser.
En général (donc dans la plupart des cours), le résultat qui dit que\,dt=\lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^nf\big(\frac{k}{n}\big)) , ben il est précédé de "Pour toute fonction continue
, ben il est précédé de "Pour toute fonction continue 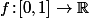 ".
".
Or la fonction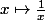 n'est pas une fonction continue
n'est pas une fonction continue 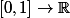 donc soit tu dispose d'un théorème "plus puissant" que celui là (mais lequel ?), soit tout ce que tu peut faire, c'est de "t'inspirer" de la preuve du théorème pour montrer la divergence de la série et dans ce cas, tu revient peu ou prou à la preuve classique vu que la preuve du théorème en question, ben elle procède exactement de la même façon que la preuve "usuelle" de la divergence de la série harmonique.
donc soit tu dispose d'un théorème "plus puissant" que celui là (mais lequel ?), soit tout ce que tu peut faire, c'est de "t'inspirer" de la preuve du théorème pour montrer la divergence de la série et dans ce cas, tu revient peu ou prou à la preuve classique vu que la preuve du théorème en question, ben elle procède exactement de la même façon que la preuve "usuelle" de la divergence de la série harmonique.
EDIT : En fait, ce que tu peut utiliser comme "théorème", c'en serait un qui donne une majoration/minoration de la somme par rapport à l'intégrale modulo de supposer f monotone. Sauf que là, la preuve de ce nouveau théorème, ben ça devient très très exactement la même que celle de la divergence de la série harmonique...
Le problème, c'est de savoir quel théorème tu compte utiliser.
En général (donc dans la plupart des cours), le résultat qui dit que
Or la fonction
EDIT : En fait, ce que tu peut utiliser comme "théorème", c'en serait un qui donne une majoration/minoration de la somme par rapport à l'intégrale modulo de supposer f monotone. Sauf que là, la preuve de ce nouveau théorème, ben ça devient très très exactement la même que celle de la divergence de la série harmonique...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Hn
Bonjour
Je vais peut être rien apprendre à personne (vu que c'est classique) mais la série harmonique diverge car la suites des sommes partielles n'est pas de Cauchy. En effet+...+1/(2n)\geq n*1/(2n)=1/2.)
J'aime bien rappeler c'est courte démo qui est liée avec la complétude de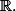
Je vais peut être rien apprendre à personne (vu que c'est classique) mais la série harmonique diverge car la suites des sommes partielles n'est pas de Cauchy. En effet
J'aime bien rappeler c'est courte démo qui est liée avec la complétude de
Re: Hn
si on peut faire une limite, on peut en faire 2.
soit ε >0
f(x)=1/x est parfaitement continue sur [ε;1]
soit no tel que 1/no < ε
tu as que l'intégrale de ε à 1 de f est plus petite que ta somme
ensuite tu fais tendre n vers l'infini.
tu intégrale est bien définie et dépend de ε
puis tu fais tendre ε ver 0, ou tu minores ta somme en fonction de ε.
tu vas avoir que ta somme est aussi grande que tu veux
Variante : tu pars de M grand.
tu choisis epsilon pour que ton intégrale soit plus grande que M
tu minores ta somme par ton intégrale
ta somme est minorée par M, aussi grand que tu veux
Re: Hn
Je continue à penser que c'est vraiment "se faire c..." pour pas grand chose que d'absolument vouloir utiliser le théorème en question plutôt que de simplement "s'inspirer" de la preuve pour en refaire une complète (i.e. n'utilisant pas le théorème en question).
Par exemple là :
Si on ne fait que et exclusivement que appliquer le théorème sous sa forme "basique" (avec f continue), on ne peut l'applique que sur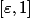 , et il dit que
, et il dit que \,dt=\lim_{n\to\infty}\frac{1-\varepsilon}{n}\sum_{k=1}^nf\big(\varepsilon+k\frac{1-\varepsilon}{n}\big))
Et si tu utilise la monotonie de f:x->1/x, pour minorer, alors là, tu revient très précisément à la preuve classique (*) de la divergence de Hn (sauf que tu as fait un changement de variable qui en fait... ne sert à rien...)
(*) Où, depuis le début, ce que j'appelle "la preuve classique", c'est la minoration du 1/k de Hn par l'intégrale de k-1 à k de 1/t dt, c'est à dire une comparaison série/intégrale.
Par exemple là :
Tu le justifie comment que l'intégrale est plus petite que la somme ?pascal16 a écrit:tu as que l'intégrale de ε à 1 de f est plus petite que ta somme
Si on ne fait que et exclusivement que appliquer le théorème sous sa forme "basique" (avec f continue), on ne peut l'applique que sur
Et si tu utilise la monotonie de f:x->1/x, pour minorer, alors là, tu revient très précisément à la preuve classique (*) de la divergence de Hn (sauf que tu as fait un changement de variable qui en fait... ne sert à rien...)
(*) Où, depuis le début, ce que j'appelle "la preuve classique", c'est la minoration du 1/k de Hn par l'intégrale de k-1 à k de 1/t dt, c'est à dire une comparaison série/intégrale.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Hn
Pour dire la même chose de façon à peine différente, la preuve classique, elle repose sur la comparaison de la série harmonique avec l'intégrale 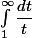 .
.
Certes, cette intégrale à le mauvais goût de ne pas être une intégrale sur un segment (=intervalle fermé borné) donc il peut venir à l'esprit de se ramener à une intégrale sur un segment, à savoir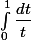 .
.
Sauf que ça simplifie que dalle vu que la fonction qu'on intègre n'est pas continue sur le segment, donc on a affaire à une "intégrale impropre" et le fait que l'intervalle d'intégration soit un segment n'a plus le moindre intérêt (ça ne simplifie absolument rien pour les intégrales impropres).
Certes, cette intégrale à le mauvais goût de ne pas être une intégrale sur un segment (=intervalle fermé borné) donc il peut venir à l'esprit de se ramener à une intégrale sur un segment, à savoir
Sauf que ça simplifie que dalle vu que la fonction qu'on intègre n'est pas continue sur le segment, donc on a affaire à une "intégrale impropre" et le fait que l'intervalle d'intégration soit un segment n'a plus le moindre intérêt (ça ne simplifie absolument rien pour les intégrales impropres).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
