Est ce que
Toologie : Adhérence et convexité
13 messages
- Page 1 sur 1
Toologie : Adhérence et convexité
A et B sont deux parties convexes et bornées du plan complexe tq :
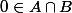
 et
et 
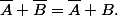
Est ce que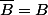 ?
?
Est ce que
Re: Toologie : Adhérence et convexité
Tu as déjà eu une réponse positive sur les-mathématiques.net. Pourquoi viens-tu reposer la même question ici ?
L'hypothèse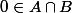 est inutile, il suffit d'avoir
est inutile, il suffit d'avoir  et
et  non vides. C'est aussi valable dans n'importe quel
non vides. C'est aussi valable dans n'importe quel  .
.
L'hypothèse
Re: Toologie : Adhérence et convexité
Salam et bonjour,
En fait, c'est dans ce forum que j'ai posté cette question pour la première fois, tu peux consulter la date de diffusion. La réponse donnée dans le forum des mathématiques-net étudie seulement le cas où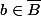 extremal, et si
extremal, et si  n'est pas extremal ? Et s'il y'a une meilleure solution, pourquoi pas !et que tout le monde en profite que ce soit dans un forum ou dans un autre.....
n'est pas extremal ? Et s'il y'a une meilleure solution, pourquoi pas !et que tout le monde en profite que ce soit dans un forum ou dans un autre.....
En fait, c'est dans ce forum que j'ai posté cette question pour la première fois, tu peux consulter la date de diffusion. La réponse donnée dans le forum des mathématiques-net étudie seulement le cas où
Re: Toologie : Adhérence et convexité
Eh bien, en regardant les dates, je vois que tu as eu la réponse sur les-mathématiques.net le 1er juillet à 2:25, et que tu es venu poster la même question ici le 2 juillet à 15:12.
Pourquoi ne pas reconnaître tout simplement que tu n'as pas compris la réponse ? Pourquoi ne pas demander des explications là où la réponse t'a été apportée ?
Un élément d'explication qui aurait alors pu t'être donné : si est convexe borné dans un
est convexe borné dans un  , alors
, alors 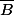 est convexe compact et est donc l'enveloppe convexe de ses points extrémaux (Krein-Milman). Il suffit donc que tout point extrémal de
est convexe compact et est donc l'enveloppe convexe de ses points extrémaux (Krein-Milman). Il suffit donc que tout point extrémal de 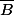 appartienne à
appartienne à  pour que
pour que 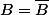 .
.
Une fois ceci établi, on montre par récurrence sur la dimension de l'espace ambiant que si
de l'espace ambiant que si  est un point extrémal de
est un point extrémal de 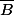 , alors il existe
, alors il existe 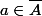 tel que, pour tous
tel que, pour tous 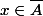 et
et 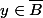 , si
, si 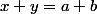 alors
alors 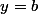 .
.
Pourquoi ne pas reconnaître tout simplement que tu n'as pas compris la réponse ? Pourquoi ne pas demander des explications là où la réponse t'a été apportée ?
Un élément d'explication qui aurait alors pu t'être donné : si
Une fois ceci établi, on montre par récurrence sur la dimension
Re: Toologie : Adhérence et convexité
Salam et bonjour,
D'abord, merci bp pour les explications. Je suis formel pour la date : c'est en 26/06/2016 à 17:16 que j'ai posté cette question . Tu peux le vérifier en consultant cette adresse cafe-mathematique/topologie-adherence-convexite-t175223.html. Tu n'as qu'à copier coller dans votre navigateur, ou un simple clic de votre par!
Tu peux consulter aussi cette adresse :http://www.les-mathematiques.net/phorum/read.php?14,1292917 pour savoir que je peux dire "je n'ai pas compris".
D'abord, merci bp pour les explications. Je suis formel pour la date : c'est en 26/06/2016 à 17:16 que j'ai posté cette question . Tu peux le vérifier en consultant cette adresse cafe-mathematique/topologie-adherence-convexite-t175223.html. Tu n'as qu'à copier coller dans votre navigateur, ou un simple clic de votre par!
Tu peux consulter aussi cette adresse :http://www.les-mathematiques.net/phorum/read.php?14,1292917 pour savoir que je peux dire "je n'ai pas compris".
Modifié en dernier par bagabd le 03 Juil 2016, 13:16, modifié 1 fois.
Re: Toologie : Adhérence et convexité
Tu as beau ergoter, ceci ne change rien au fait que tu as posté ici la même question après avoir eu une réponse sur les-mathématiques.net, sans rien dire du fait que tu avais déjà eu une réponse.
As-tu compris cette réponse, maintenant ?
As-tu compris cette réponse, maintenant ?
Re: Toologie : Adhérence et convexité
Salam et bonjour,
à vrai dire pas encore. Peux tu me rédiger une preuve complète en dimension 2 ( plan complexe) et merci d'avance.
à vrai dire pas encore. Peux tu me rédiger une preuve complète en dimension 2 ( plan complexe) et merci d'avance.
Re: Toologie : Adhérence et convexité
Je te propose plutôt un plan de travail. Raisonner dans le plan complexe ou dans un  quelconque ne change rien.
quelconque ne change rien.
Première étape :
Soient et
et  deux compacts convexes non vides de
deux compacts convexes non vides de  . Soit
. Soit  un point extrémal de
un point extrémal de  . On veut montrer qu'il existe un point
. On veut montrer qu'il existe un point  [de
[de  - coquille signalée par bagabd] de
- coquille signalée par bagabd] de  tel que, pour tous
tel que, pour tous  de
de  et
et  de
de  , si
, si 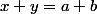 alors
alors 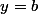 . On va démontrer cette assertion par récurrence sur
. On va démontrer cette assertion par récurrence sur  .
.
1°) Initialisation pour : je te laisse faire (rappel : les compacts convexes de
: je te laisse faire (rappel : les compacts convexes de  sont les intervalles fermés bornés, dont les points extrémaux sont les extrémités).
sont les intervalles fermés bornés, dont les points extrémaux sont les extrémités).
2°) Hérédité : on suppose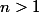 , le résultat établi dans
, le résultat établi dans 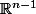 , on veut le montrer dans
, on veut le montrer dans 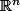 .
.
On peut sans perte de généralité supposer que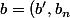\in \R^{n-1}\times \R) est tel que
est tel que 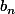 est le maximum des
est le maximum des  -èmes coordonnées de points de
-èmes coordonnées de points de  (quitte à faire un changement linéaire de coordonnées). Soit
(quitte à faire un changement linéaire de coordonnées). Soit  le maximum des
le maximum des  -èmes coordonnées des points de
-èmes coordonnées des points de  .
.
On pose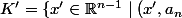\in K\}) et
et 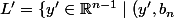\in L\}) . Montrer que
. Montrer que 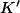 et
et 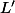 sont des convexes compacts non vides de
sont des convexes compacts non vides de 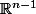 et que
et que 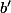 est un point extrémal de
est un point extrémal de 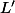 . Appliquer alors l'hypothèse de récurrence pour
. Appliquer alors l'hypothèse de récurrence pour 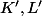 et
et 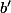 et conclure pour
et conclure pour  ,
,  et
et  .
.
Deuxième étape :
Soient et
et  des convexes bornés non vides de
des convexes bornés non vides de  tels que
tels que 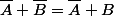 . Montrer que tout point extrémal de
. Montrer que tout point extrémal de 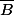 appartient à
appartient à  (bien sûr, utiliser le résultat de la première étape). Conclure que
(bien sûr, utiliser le résultat de la première étape). Conclure que 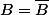 .
.
Tu peux bien sûr t'aider des explications de Siméon sur les-mathématiques.net. Le plan de travail que je te propose n'est qu'une présentation légèrement différente des mêmes idées.
Première étape :
Soient
1°) Initialisation pour
2°) Hérédité : on suppose
On peut sans perte de généralité supposer que
On pose
Deuxième étape :
Soient
Tu peux bien sûr t'aider des explications de Siméon sur les-mathématiques.net. Le plan de travail que je te propose n'est qu'une présentation légèrement différente des mêmes idées.
Modifié en dernier par Robot le 03 Juil 2016, 21:03, modifié 1 fois.
Re: Toologie : Adhérence et convexité
Salam, bonjour et merci
dans la preuve que tu as donnée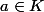 .
.
d'autre part, peut on prendre dés le début est aussi extrémal de
est aussi extrémal de 
pour assurer l 'hérédité?
dans la preuve que tu as donnée
d'autre part, peut on prendre dés le début
pour assurer l 'hérédité?
Re: Toologie : Adhérence et convexité
Salam,
Salam est l'un des noms du dieu, donc
Salam= la paix absolue.
Salam est l'un des noms du dieu, donc
Salam= la paix absolue.
Re: Toologie : Adhérence et convexité
Je ne vois pas ce que vient faire ton dernier message ici. Reste sur les mathématiques.
As-tu essayé de mettre en oeuvre le plan de travail que je t'ai donné ? Tu verras qu'il n'y rien besoin de dire sur d'autre que ce que j'ai écrit pour assurer l'hérédité.
d'autre que ce que j'ai écrit pour assurer l'hérédité.
As-tu essayé de mettre en oeuvre le plan de travail que je t'ai donné ? Tu verras qu'il n'y rien besoin de dire sur
Re: Toologie : Adhérence et convexité
Salam, bonjour
tu m'as demandé de t'expliquer la signification du mot salam dans un message qui est vite effacé et je l'ai expliquée.
Dans le plan de la preuve "première étape", je crois au lieu d' écrire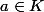 , il a été écrit
, il a été écrit 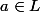 .
.
Et merci encore une fois.
tu m'as demandé de t'expliquer la signification du mot salam dans un message qui est vite effacé et je l'ai expliquée.
Dans le plan de la preuve "première étape", je crois au lieu d' écrire
Et merci encore une fois.
Re: Toologie : Adhérence et convexité
tu m'as demandé de t'expliquer la signification du mot salam dans un message qui est vite effacé et je l'ai expliquée.
Tu as des hallucinations ?
Dans le plan de la preuve "première étape", je crois au lieu d' écrire, il a été écrit
Exact, je corrige la coquille.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
