Tirages sans remise et réinitialisation
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
oxi
- Messages: 5
- Enregistré le: 21 Oct 2022, 11:42
-
 par oxi » 21 Oct 2022, 12:06
par oxi » 21 Oct 2022, 12:06
Bonjour à tous,
Je joue à un jeu et je n'arrive pas à modéliser mathématiquement le nombre d'essais nécessaires en moyenne pour obtenir 100 objets.
Il s'agit d'un jeu où il y a un tableau de récompenses composé de 9 cases avec 1 seule case où il y a l'objet que je souhaite.
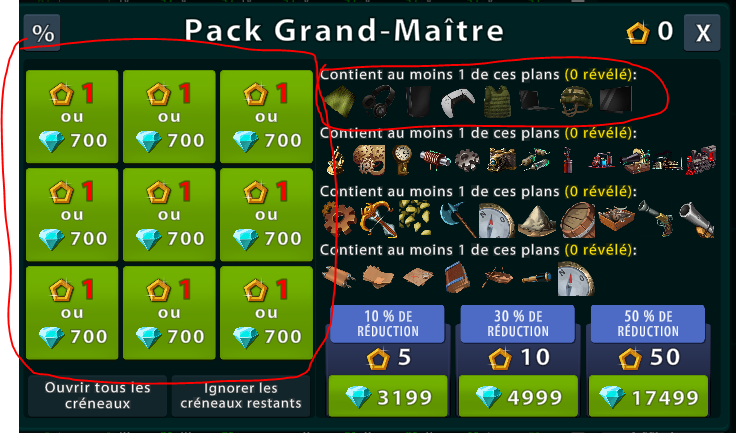
Je peux réinitialiser le tableau quand je le souhaite (à l'aide du bouton "ignorer les créneaux restants"), si bien que je le fais dès que j'ai obtenu mon objet. Et que je continue de découvrir les cases dans le cas inverse (puisque mes chances d'obtenir le jeton augmente à chaque fois : 1/9 puis 1/8 puis 1/7 etc...).
Mes souvenirs de lycée me permettent de calculer facilement le résultat si je ne réinitialise pas. Mais, je ne vois pas comment modéliser avec la réinitialisation.
Existe t'il une formule pour le calculer?
Merci!
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Oct 2022, 13:22
par GaBuZoMeu » 21 Oct 2022, 13:22
Bonjour,
Je ne comprends pas trop ton jeu.
Sur une situation plus claire : dans une urne il y a 8 boules blanches et une rouge. On tire sans remise. Quelle est l'espérance du nombre de tirages à faire pour obtenir la boule rouge ?
Je te laisse répondre à cette question.
-
oxi
- Messages: 5
- Enregistré le: 21 Oct 2022, 11:42
-
 par oxi » 21 Oct 2022, 15:05
par oxi » 21 Oct 2022, 15:05
Bonjour GaBuZoMeu et merci pour cette réponse. C'est effectivement la modélisation que je cherche avec comme difficulté supplémentaire :
Quand je trouve la boule rouge, j'arrête les tirages (puisqu'il n'y a plus de boule rouge et donc que je n'ai plus d'intérêt de continuer), je remets toutes les boules et je recommence à tirer. Quelle est alors l'espérance?
Pour répondre à ta question (qui ne prend donc pas en compte l'aspect réinitialisation de ma question), selon moi (souvenir qui date d'une vingtaine d'années. C'est donc peut être complétement faux), j'ai :
- 1/9 d'obtenir la boule rouge au premier tirage
- 1/9 d'obtenir la boule rouge au deuxième tirage (1 /8 d'obtenir la boule rouge et 8 /9 chance de ne pas avoir obtenu de boule rouge au premier tirage 8 /9*1 /8)
-1/9 d'obtenir la boule rouge au troisième tirage (8 /9*7/8*1/7)
...
- 1/9 d'obtenir la boule rouge au 9ième tirage (8 /9*7/8*6/7*...*1/2*1)
Je dirais donc que l'espérance est de 1/9+2*1/9+...+9*1/9= (9*10/2)/9=5
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Oct 2022, 15:26
par GaBuZoMeu » 21 Oct 2022, 15:26
Dommage, tu n'as pas du tout éclairci la situation de ton jeu.
Alors, je continue sur la modélisation que j'ai commencé à utiliser. Tu as bien trouvé l'espérance du nombre de tirages pour trouver la boule rouge : 5
Maintenant supposons qu'on répète la recherche de boules rouges : à chaque fois qu'on en trouve une, on enlève l'urne où on vient de la trouver même si elle contient encore des boules et on apporte une nouvelle urne contenant 9 boules dont une rouge.
Quelle est l'espérance du nombre total de tirages pour trouver 100 boules rouges (rappel : l'espérance est additive).
-
oxi
- Messages: 5
- Enregistré le: 21 Oct 2022, 11:42
-
 par oxi » 21 Oct 2022, 15:31
par oxi » 21 Oct 2022, 15:31
Merci GaBuZoMeu pour cette réponse.
La deuxième question que tu viens de poser correspond à l'énoncé de mon problème que j'ai du mal à modéliser correctement.
De façon simpliste je dirais 500 (je reproduis 100 fois ma première expérience). Mais je ne suis pas convaincu que se soit la bonne réponse (?)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Oct 2022, 16:22
par GaBuZoMeu » 21 Oct 2022, 16:22
Je t'ai pourtant donné l'argument de l'additivité de l'espérance !
Soit

la variable aléatoire qui est le nombre de tirages dans la

-ème urne pour en extraire la boule rouge. Le nombre total de tirages pour récupérer les 100 boules rouges est

. Par additivité de l'espérance,
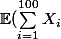=\sum_{i=1}^{100} \mathbb E(X_i))
. Or tu connais
)
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Oct 2022, 16:27
par GaBuZoMeu » 21 Oct 2022, 16:27
Tu peux aussi calculer des variances et, en utilisant le théorème central limite, avoir une bonne approximation de la loi du nombre total de tirages pour avoir les 100 boules rouges par une loi normale.
-
oxi
- Messages: 5
- Enregistré le: 21 Oct 2022, 11:42
-
 par oxi » 21 Oct 2022, 16:43
par oxi » 21 Oct 2022, 16:43
Merci GaBuZoMeu pour toutes ces explications didactiques. Pour être sûr de bien comprendre ta conclusion.
La réponse est donc 500 pour i=100?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Oct 2022, 16:47
par GaBuZoMeu » 21 Oct 2022, 16:47
Oui,

. En doutes-tu ?
-
oxi
- Messages: 5
- Enregistré le: 21 Oct 2022, 11:42
-
 par oxi » 21 Oct 2022, 16:51
par oxi » 21 Oct 2022, 16:51
A vrai dire, non

. Je voulais surtout confirmer que j'avais bien compris ce que tu avais dit.
Merci pour toutes ces explications.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 21 Oct 2022, 17:24
par GaBuZoMeu » 21 Oct 2022, 17:24
La variance du nombre de tirages pour une urne est 6,67.
La nombre de tirages pour les 100 boules rouges suit à peu près une loi normale d'espérance 500 et de variance 667 (d'écart type 25,8).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités

