Theorie de la mesure !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Déc 2007, 19:54
par barbu23 » 17 Déc 2007, 19:54
Bonsoir :
Dans l'espace

muni de la norme :

...
Pourquoi :
 = N_{\infty}(g) \hspace{10cm} \Longleftrightarrow \hspace{10cm} f = g \hspace{10cm} \mu - $)
p.p. ?
Bon, il est clair que :

p.p.
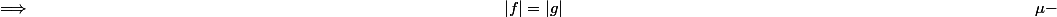
p.p.
 = N_{\infty}(g) $)
Mais, la reciproque, je sais pas comment faire !
Merci d'avance de votre aide !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 17 Déc 2007, 19:58
par tize » 17 Déc 2007, 19:58
Bonjour,
c'est bien sur faux, prendre f=-1 et g=1, ça doit être N(f-g)=0 <=> f=g pp
-
BQss
- Membre Irrationnel
- Messages: 1202
- Enregistré le: 02 Nov 2006, 03:32
-
 par BQss » 17 Déc 2007, 20:01
par BQss » 17 Déc 2007, 20:01
Salut,
et c'est aussi faux pour Lp et pour un EV normé en general, je sais pas pourquoi tu voulais prouver ca.
peut-etre que tu pensais a ||f||=0 <-> f=0 p.p
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Déc 2007, 20:02
par barbu23 » 17 Déc 2007, 20:02
Si
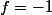
et
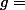
alors

n'est pas égale à

- p.p. ... !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 17 Déc 2007, 20:04
par tize » 17 Déc 2007, 20:04
barbu23 a écrit:Si
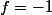
et
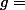
alors

n'est pas égale à

- p.p. ... !!
Bah non puisqu'elles sont différentes partout !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Déc 2007, 20:06
par barbu23 » 17 Déc 2007, 20:06
tize a écrit:Bonjour,
c'est bien sur faux, prendre f=-1 et g=1
Donc, c'est pas correct ton contre exemple !
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 17 Déc 2007, 20:09
par tize » 17 Déc 2007, 20:09
Bah si puisque N(f)=N(g)=1 !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Déc 2007, 20:12
par barbu23 » 17 Déc 2007, 20:12
Ah oui, c'est vrai ! merci beaucoup !! :lol2:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Déc 2007, 11:45
par barbu23 » 18 Déc 2007, 11:45
Bonjour :
Proposition :Soit
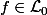
.
On a :
 = \displaystyle \inf_{N \in \mathcal{N}} \displaystyle \sup_{x \not \in N} |f(x)| $)
.
où :

est la famille des negligeables dans

( tribu ).
Preuve : \leq \displaystyle \sup_{x \not \in N} |f(x)| $)
En prenant la borne inferieure sur

, on obtient :
 \leq \displaystyle \inf_{N \in \mathcal{N}} \displaystyle \sup_{x \not \in N} |f(x)| $)
.
Reciproquement :
Montrons que :
| \leq N_{\infty}(f) $)
Soit :
| $)
Alors :
| $)

.
Or :
| : N \in \mathcal{N} \} $)
est la plus petite famille des majorants
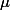
p.p. de
 $)
Donc :

.
Par conséquent :
 = \displaystyle \inf_{N \in \mathcal{N}} \displaystyle \sup_{x \not \in N} |f(x)| $)
.
Questions : $)
Pouvez vous m'expliquer pourquoi , dans la demonstration,
| : N \in \mathcal{N} \} $)
est la plus petite famille des majorants
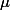
p.p. de
 $)
 $)
Pourquoi :
 \leq \displaystyle \sup_{x \not \in N} |f(x)| $)
Merci d'avance !
P.S :
 = \displaystyle \inf \{ \hspace{20cm} M \in \mathbb{R}^{+} \bigcup \{ +\infty \} \hspace{10cm} : \hspace{10cm} |f| \leq M \hspace{10cm} \mu - $)
p.p.

-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Déc 2007, 12:30
par barbu23 » 18 Déc 2007, 12:30
Pour

:
Si

existe, alors :
| \leq \displaystyle \sup_{x \not \in N } |f(x)| $)
avec :

le plus grand negligeable qui existe ! n'est ce pas ?!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 18 Déc 2007, 19:58
par barbu23 » 18 Déc 2007, 19:58
Help pls !
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 18 Déc 2007, 20:11
par Lierre Aeripz » 18 Déc 2007, 20:11
Quelle est ta définition de
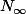
?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 19 Déc 2007, 00:53
par barbu23 » 19 Déc 2007, 00:53
Salut :
Regarde le message n° 9, c'est en bas !
c'est la seule norme qu'il y'a dans mon cours ,associé à :

!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités