Théorie des modules !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Jan 2009, 12:33
par barbu23 » 16 Jan 2009, 12:33
Bonjour :
Voiçi un Théorème de mon cours sur les modules que je comprends pas la démonstration ! Vueillez m'aider, et merci mille fois !
Théorème :
Soit

un anneau et
_{s} $)
une famille de

modules.
Pour tout

module

, et toute famille
_{s} $)
de mrophismes :

, il existe un unique morphisme

tel que pour tout

:
 Démonstration
Démonstration :
Posons :
= (m_{s})_{s} = (f_{s}(m))_{s} $)
Montrons que :

est un homomorphisme de

modules.

:
 = (f_{s}(a.m+b.n))_{s} = (a.f_{s}(m)+b.f_{s}(n))_{s} = a.(f_{s}(m))_{s}+b.(f_{s}(n))_{s} = a.f(m)+b.f(n) $$)
Supposons que :

verifie

.
Alors si :
= (m_{s})_{s} $)
, on a nacessairement :
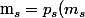_{s}) = p_{s}(f(m)) = p_{s} \circ f(m) = f_{s}(m) $)
.
ce qui montre que

est unique.
Question :
J'arrive pas encore à comprendre le passage où il est dit que

est unique ! Quelle propriété a-t-on utilisé pour montrer l'unicité de

?
Merci infiniment !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 16 Jan 2009, 15:15
par Doraki » 16 Jan 2009, 15:15
Ils ont dit que si on suppose que pour tout s, ps composé avec f = fs,
alors pour tout s et pour tout m, ps(f(m)) = fs(m)
f(m) est un élément du produit des Mi donc f(m) est une famille (mi) avec ms dans Ms.
Donc pour tout s et pour tout m, fs(m) = ps(f(m)) = ps( (mi) ) = ms.
Donc en fait, pour tout m, f(m) est la famille des fs(m).
Donc y'a pas de choix possible pour les valeurs de f.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 16 Jan 2009, 16:42
par yos » 16 Jan 2009, 16:42
Existence de f :
barbu23 a écrit:Posons :
= (m_{s})_{s} = (f_{s}(m))_{s} $)
Montrons que :

est un homomorphisme de

modules.

:
 = (f_{s}(a.m+b.n))_{s} = (a.f_{s}(m)+b.f_{s}(n))_{s} = a.(f_{s}(m))_{s}+b.(f_{s}(n))_{s} = a.f(m)+b.f(n) $$)
Unicité de f :
barbu23 a écrit:Supposons que :

verifie

.
Alors si :
= (m_{s})_{s} $)
, on a nacessairement :
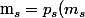_{s}) = p_{s}(f(m)) = p_{s} \circ f(m) = f_{s}(m) $)
.
ce qui montre que

est unique.
La première ligne de la partie unicité signifie : "soit f comme il faut".
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 17 Jan 2009, 18:11
par barbu23 » 17 Jan 2009, 18:11
Salut "Doraki" et "yos" :
Ce que j'ai pas encore compris, est le passage suivant :
on a nacessairement :
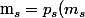_{s}) = p_{s}(f(m)) = p_{s} \circ f(m) = f_{s}(m) $)


est unique.
Ce qu'on fait la plupart du temps pour montrer l'unicité l'unicité d'un objet, on considère un deuxième objet, et on fait un petit developpement de calcul jusqu'à ce qu'on arrive à une égalité entre ces deux objets, mais ici, ils font rien de tout celà ! Je ne sais pas pourquoi, c'est encore obscure ce passage !
Merci d'avance de votre aide !
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 17 Jan 2009, 18:44
par Doraki » 17 Jan 2009, 18:44
On a M, M1, M2...Mk des A-modules, f1,f2...fk des morphismes, fi : M -> Mi.
Y'a combien de morphismes (ou même de fonctions) f : M -> M1 * M2 ... * Mk
telles que pour tout m de M, f(m) = (f1(m),f2(m)....fk(m)) ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 17 Jan 2009, 18:48
par yos » 17 Jan 2009, 18:48
barbu23 a écrit:Ce qu'on fait la plupart du temps pour montrer l'unicité d'un objet, on considère un deuxième objet, et on fait un petit developpement de calcul jusqu'à ce qu'on arrive à une égalité entre ces deux objets,
Non, il y a d'autres façons de prouver l'unicité. Souvent, on prouve l'unicité
avant l'existence dans une démonstration analyse-synthèse. C'est le plus naturel dans beaucoup de cas (y compris ici, ce serait mieux selon moi).
Le principe est :
- Analyse (ou unicité sous réserve d'existence) : supposons que l'objet K existe. Alors il vérifie ceci-cela (des conditions nécessaires qui rendent l'objet déterminé (s'il existe!)).
- Synthèse (ou existence) : considérons un objet du type ceci-cela (obtenu en fin d'analyse). On montre qu'il convient.
Ici, le prof fait l'existence en premier car on voit bien l'objet f à exhiber. Ensuite il prouve que y avait pas le choix pour f (uncité).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
