Théorie des groupes et Algebre linéaire

[Balabyss]

Bonjour, bonsoir a tous, je suis actuellement en L3 Maths et je galère sur un exo qui me fait m'arracher les cheveux...
Le voici :
Soit G un groupe et soient a,b des éléments d'ordre fini qui commutent, cad ab=ba
Le but de cet exo est de montrer que si o(a) et o(b) sont premier entre eux alors o(ab) =o(a)o(b)

je connais la notion d'ordre qui se note ici o(a)

(a) Montrer que (ab)^(o(a)o(b))=1 et en déduire que o(ab) | o(a)o(b)

(b) Posons x=o(ab) et c=a^x. Montrer que c=b^(-x) et c^(o(a))=1=c(o(b)). Déduire c=1 en utilisant Bézout
(en gros il y a un u et v tq 1=u0(a) + vo(b)

(c) Ainsi o(a)|x et o(b)|x (expliquer pourquoi). Du coup comme a et b sont premier on a o(a)o(b)|x.
Conclure

Voila,

je crois avoir réussi a moitié la a .....

j'ai mis que Si o(a) est finit, alors son ordre est le plus petit entier positif, appelons le m, tel que a^m =e
e étant l'élément neutre

on a donc pareil pour b (on note cet entier n)

(ab)^(a^(m)b^(m))=1

on a donc (ab)^(o(a)o(b))=a^(o(a)o(b)) * b^(o(a)o(b))
=a^(o(a))^(o(b)) * b^(o(b))^(o(a))
= 1^(o(b)) * 1^(o(a))
= 1

Mais je n'arrive pas a faire la suite...
Merci de votre aide a tous !

[Kolis]

Bonjour !
Connais-tu le principal (çà devrait être dans ton cours) : si alors est un multiple de l'ordre de ?

Je pose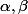 les ordres respectifs de .
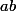Si est l'ordre de et tu as (puisque ).
Donc .

. Idem pour .
Comme tu as bien .

De là tu conclus comme demandé, à condition de connaître le résultat rappelé au début !

[Balabyss]

Oui j ai bien eu cet definition. Mais le probleme que j ai est a partir de ce fameux Bezout avec c = 1... On ne sait pas que l ordre de a et l ordre de b sont premier entre eux... donc je n arrive pas

[Ben314]

Salut,

Soit G un groupe et soient a,b des éléments d'ordre fini qui commutent, cad ab=ba
Le but de cet exo est de montrer que si o(a) et o(b) sont premier entre eux alors o(ab) =o(a)o(b)

On ne sait pas que l ordre de a et l ordre de b sont premier entre eux... donc je n arrive pas

A mon sens, le problème, c'est déjà de savoir si l'exo que tu cherche est effectivement celui que tu as donné au début (dans lequel on sait que les ordres de a et b sont premier entre eux) ou si c'est un autre exo. que tu cherche.

[Balabyss]

J'ai attendu la correction pour être certaine de mes doutes, et en effet, ils ont supposé o(a) et o(b) premier entre eux. Je n'ai pas osé utiliser cette méthode car pour moi, on cherchait a résoudre le problème justement pour amener cette conclusion. Pas s'en servir !
Mais il est vrai qu'en posant cette supposition, la réponse en devenait tout a fait logique. On se retrouvait alors avec c a la puissance ua+bv=1 comme la dit Kolis et on avait alors facilement la conclusion !
Merci a tous pour votre aide !

[Ben314]

J'ai attendu la correction pour être certaine de mes doutes, et en effet, ils ont supposé o(a) et o(b) premier entre eux. Je n'ai pas osé utiliser cette méthode car pour moi, on cherchait a résoudre le problème justement pour amener cette conclusion. Pas s'en servir !

Le problème, avant même de chercher à faire des maths., ça serait peut être de comprendre le Français.
Parce que personnellement, dans la phrase "Si on prend une souris blanche, alors elle a forcément les yeux rouges", j'ai un peu du mal à comprendre quel est le cheminement intellectuel qui t'amène à considérer que le fait que la souris soit blanche (ou pas) est une conclusion.
Et ne pas se servir de l'hypothèse "est blanche", c'est à dire passer des plombes à regarder la couleur des yeux de souris de couleur quelconque, ben je t'avoue que vu la question posée, je comprend pas trop l'intérêt non plus.