Théorie des ensembles

par **Judoboy** » 24 Fév 2012, 15:48

Bonjour à tous, j'ai commencé un cours de théorie des ensembles et certains points restent un peu obscurs pour moi :

- Pour montrer qu'aucun ensemble ne peut contenir tous les ensembles on a fait appel à Z = {X / X n'appartient pas à X}. Comment un ensemble peut-il appartenir à lui-même ? Si c'est le cas X = X U {X}, ce qui n'a aucun sens non ?

- J'ai du mal à voir si l'axiome d'extensionnalité sert à définir la relation "=" ou s'il énonce simplement une de ses propriétés.

J'aurai pas mal d'autres questions prochainement je pense. Par ailleurs si vous connaissez un bon ouvrage de théorie des ensembles je suis preneur.

P.S. : Comment on obtient les symboles mathématiques sur ce forum ?

par **Manny06** » 24 Fév 2012, 16:40

Judoboy a écrit:Bonjour à tous, j'ai commencé un cours de théorie des ensembles et certains restent un peu obscurs pour moi :

- Pour montrer qu'aucun ensemble ne peut contenir tous les ensembles on a fait appel à Z = {X / X appartient à X}. Comment un ensemble peut-il appartenir à lui-même ? Si c'est le cas X = X U {X}, ce qui n'a aucun sens non ?

- J'ai du mal à voir si l'axiome d'extensionnalité sert à définir la relation "=" ou s'il énonce simplement une de ses propriétés.

J'aurai pas mal d'autres questions prochainement je pense. Par ailleurs si vous connaissez un bon ouvrage de théorie des ensembles je suis preneur.

P.S. : Comment on les symboles mathématiques sur ce forum ?

je peux t'indiquer le livre "Théorie axiomatique des ensembles" par Jean Louis Krivine aus PUF mais il faut savoir lire entre les lignes.......
pour les symboles regarde les premiers messages de la partie Lycée

par **st00pid_n00b** » 24 Fév 2012, 17:07

Qu'un ensemble soit un élément de lui même n'est pas une contradiction. L'exemple de vulgarisation classique est une bibliothèque qui possède un catalogue de tous ses livres. Le catalogue est lui même un livre donc il apparaitra dans la liste (pour peu que le bibliothécaire soit un logicien

Mais si on suppose qu'il existe un ensemble de tous les ensemble, appelons le E, cela aboutit à une contradiction. On définit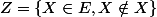

. Et là on ne peut pas répondre à la question est-ce que

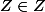? Donc l'hypothèse que E existe est fausse. C'est le paradoxe de Russel.

par **Judoboy** » 24 Fév 2012, 17:30

st00pid_n00b a écrit:Qu'un ensemble soit un élément de lui même n'est pas une contradiction. L'exemple de vulgarisation classique est une bibliothèque qui possède un catalogue de tous ses livres. Le catalogue est lui même un livre donc il apparaitra dans la liste (pour peu que le bibliothécaire soit un logicien

Ca marche pas ça.

J'ouvre le catalogue, j'ai :

- Une liste des autres livres de la bibliothèque, quand je me rends à une référence donnée j'obtiens le livre en entier.

- Le catalogue. Si j'ouvre le catalogue à l'intérieur du catalogue, j'ai le catalogue en entier qui lui-même contient :

- Une liste des autres livres de la bibliothèque, quand je me rends à une référence donnée j'obtiens le livre en entier.

- Le catalogue. Si j'ouvre le catalogue à l'intérieur du catalogue à l'intérieur du catalogue, etc.
Ca fait un livre de taille infinie...

C'est un peu ce que je disais, si on veut que X appartienne à X il faut que X = X U {X}, on s'en sort jamais ???

par **Doraki** » 24 Fév 2012, 18:07

En supposant que ZF est consistant,

Tu peux très bien avoir un modèle de ZF où il y a un ensemble qui est un élément de lui-même.
"pour tout x, x n'appartient pas à x" n'est pas une déduction logique faisable à partir des axiomes de ZF(C).
Tu peux rajouter l'axiome "il existe x tel que x appartient à x" à ZF et tu n'as pas de contradiction

Un modèle de la théorie des ensembles c'est
une structure X (une collection d'ensembles) avec une interprétation de

(une partie de X*X)
de sorte que cette structure et cette interprétation vérifie les axiomes ZF.

Si on trouve un objet x dans X tel que (x,x) est dans l'interprétation de

, et que par ailleurs elle vérifie les axiomes, ben c'est bon.
(enfin bon en vrai c'est pas possible de décrire complètement un modèle de la théorie des ensembles donc je peux pas tellement te donner d'exemple)
Si on avait un modèle descriptible, on pourrait dessiner ça en mettant 1 point pour chaque objet de une flèche de x vers y pour chaque relation d'appartenance entre ces objets (pour chaque (x,y) dans l'interprétation de

). Et un objet qui se contient lui-même serait dessiné par un objet avec une flèche qui pointe sur lui-même.

Si ça te fait vomir, tu peux te rajouter l'axiome d'antifondation, qui dit qu'on ne peut pas avoir de suite infinie d'ensembles qui se contiennent (x0 qui contient x1 qui contient x2 qui contient x3 ....).
Il me semble qu'il est indépendant de ZF donc pour les maths de tous les jours, on s'en fiche, et en fait tu l'utiliseras jamais.

par **Judoboy** » 24 Fév 2012, 18:17

Ok donc la proposition "Il existe un ensemble qui se contient" est indécidable en fait ? Et pour l'axiome d'antifondation, c'est pas contradictoire avec la construction de N ?

par **Doraki** » 24 Fév 2012, 18:32

oui c'est indécidable.
Ca ne contredit pas la construction de N, parceque à partir de N tu ne peux pas obtenir une suite infinie "décroissante" d'ensembles.
A partir de N tu peux construire des suites décroissantes aussi longue que tu veux, mais y'en a pas d'infini. Au moment où tu choisis un élément de N pour ton 2ème ensemble, bah t'aterris dans un nombre entier et de là tu ne peux pas faire une suite infinie.

par **Manny06** » 24 Fév 2012, 18:37

Doraki a écrit:En supposant que ZF est consistant,

Tu peux très bien avoir un modèle de ZF où il y a un ensemble qui est un élément de lui-même.
"pour tout x, x n'appartient pas à x" n'est pas une déduction logique faisable à partir des axiomes de ZF(C).
Tu peux rajouter l'axiome "il existe x tel que x appartient à x" à ZF et tu n'as pas de contradiction

Un modèle de la théorie des ensembles c'est
une structure X (une collection d'ensembles) avec une interprétation de (une partie de X*X)
de sorte que cette structure et cette interprétation vérifie les axiomes ZF.

Si on trouve un objet x dans X tel que (x,x) est dans l'interprétation de , et que par ailleurs elle vérifie les axiomes, ben c'est bon.
(enfin bon en vrai c'est pas possible de décrire complètement un modèle de la théorie des ensembles donc je peux pas tellement te donner d'exemple)
Si on avait un modèle descriptible, on pourrait dessiner ça en mettant 1 point pour chaque objet de une flèche de x vers y pour chaque relation d'appartenance entre ces objets (pour chaque (x,y) dans l'interprétation de ). Et un objet qui se contient lui-même serait dessiné par un objet avec une flèche qui pointe sur lui-même.

Si ça te fait vomir, tu peux te rajouter l'axiome d'antifondation, qui dit qu'on ne peut pas avoir de suite infinie d'ensembles qui se contiennent (x0 qui contient x1 qui contient x2 qui contient x3 ....).
Il me semble qu'il est indépendant de ZF donc pour les maths de tous les jours, on s'en fiche, et en fait tu l'utiliseras jamais.

ce shéma avec des flèches est exactement ce qui figure dans le livre de JL Krivine

par **st00pid_n00b** » 24 Fév 2012, 20:48

@Judoboy:

Quand tu parles de "taille infinie", tu ne définis pas ce qu'est la "taille". Dirais tu que l'ensemble {{1;2};3} est "plus grand" que {1;2} ?

Pour un ensemble, on parle de cardinalité, et les 2 ensembles ci dessus ont même cardinalité (2). Dans mon exemple de catalogue, si la bibliothèque contient un nombre fini de livres, la cardinalité du catalogue sera finie elle aussi. Et d'autre part, on peut très bien avoir des ensembles de cardinalité infinie.

J'ai compris que ce qui te pose problème c'est l'aspect poupées russes infiniment emboitées. Doraki t'a donné une réponse plus technique, et il est plus calé que moi.

Théorie des ensembles

Théorie des ensembles

Qui est en ligne