Théorie des ensembles et application
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sarra_sonia
- Membre Naturel
- Messages: 66
- Enregistré le: 20 Jan 2015, 17:33
-
 par Sarra_sonia » 02 Mai 2018, 11:19
par Sarra_sonia » 02 Mai 2018, 11:19
Bonjour,
Soit
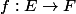
(F et F deux ensembles non vides) une application et soit A et B deux ensembles avec
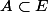
et
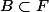
Je veux montrer que
)=f(A)\cap B)
Est ce qu'il est nécessaire de démontrer la double inclusion?
D'autre part, je sais que
\subset f(A) \cap f(B))
et que
) \subset B)
mais je ne sais pas comment les utiliser dans la démonstration!
Merci d'avance.
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 24 Juin 2018, 10:38
par hdci » 24 Juin 2018, 10:38
Bonjour,
De façon générale, démontrer l'égalité de deux ensembles par une double inclusion est une bonne méthode, qui évite de tomber dans les pièges d'une mauvaise "fausse équivalence".
Regarde donc ce qui se passe quand
)
puis quand
\cap B)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
mathelot
 par mathelot » 25 Juin 2018, 15:10
par mathelot » 25 Juin 2018, 15:10
Sarra_sonia a écrit:Bonjour,
Soit
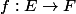
(F et F deux ensembles non vides) une application et soit A et B deux ensembles avec
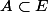
et
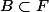
Je veux montrer que
)=f(A)\cap B)
1er cas :
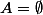
ou
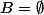
l'égalité est vraie.
2eme cas A et B non vides
si
))
il existe x tel que
 \in B)
 \in f(A))
et
 \in B)
 \in f(A) \cap B)
 \cap B)
) \subset f(A) \cap B)
réciproquement,
si
 \cap B)
il existe x tel que:
)
et
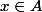
et
 \in B)
)
et
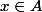
 \cap A)
 \in f(f^{-1}(B) \cap A))
 \cap A))
 \cap B \subset f(A \cap f^{-1}(B)))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
(F et F deux ensembles non vides) une application et soit A et B deux ensembles avec
et
)=f(A)\cap B)