Je suppose qu'il faut montrer en premier que f(x) est irréductible dans Z/5Z mais je n'y arrive pas. Si on suppose que f(x) n'est pas irréductible, alors il peut s'écrire comme le produit de deux polynômes non-inversibles. Je ne parviens pas a trouver de contradiction. Pouvez-vous m'aider? Merci!
Théorie des anneaux
5 messages
- Page 1 sur 1
Théorie des anneaux
Bonsoir, je souhaite montrer que {Z/5Z}/⟨f(x)⟩ est un corps, de caractéristique 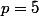 , et contenant
, et contenant 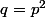 éléments, avec
éléments, avec =x^2-bx-a) .
.
Je suppose qu'il faut montrer en premier que f(x) est irréductible dans Z/5Z mais je n'y arrive pas. Si on suppose que f(x) n'est pas irréductible, alors il peut s'écrire comme le produit de deux polynômes non-inversibles. Je ne parviens pas a trouver de contradiction. Pouvez-vous m'aider? Merci!
Je suppose qu'il faut montrer en premier que f(x) est irréductible dans Z/5Z mais je n'y arrive pas. Si on suppose que f(x) n'est pas irréductible, alors il peut s'écrire comme le produit de deux polynômes non-inversibles. Je ne parviens pas a trouver de contradiction. Pouvez-vous m'aider? Merci!
Re: Théorie des anneaux
Salut,
Vu que ton polynôme est le polynôme unitaire de degré 2 générique (i.e. absolument quelconque : tu n'a aucune hypothèses sur a et b), il est évident qu'il ne peut pas être systématiquement irréductible. Si tu développe par exemple (X-2)(X-1) c'est bien clair que le résultat est un polynôme de degré 2 non irréductible !!!!!!
Sinon, pour les polynômes de degré deux (et trois), "être irréductible" c'est la même chose que "ne pas avoir de racine".
Et tu as du voir dés le Lycée ce qu'on appelle "la forme canonique" d'un polynôme du second degré qui permet de voir qu'un tel polynôme admet des racines si et seulement si son discriminant est un carré du corps considéré.
Vu que ton polynôme est le polynôme unitaire de degré 2 générique (i.e. absolument quelconque : tu n'a aucune hypothèses sur a et b), il est évident qu'il ne peut pas être systématiquement irréductible. Si tu développe par exemple (X-2)(X-1) c'est bien clair que le résultat est un polynôme de degré 2 non irréductible !!!!!!
Sinon, pour les polynômes de degré deux (et trois), "être irréductible" c'est la même chose que "ne pas avoir de racine".
Et tu as du voir dés le Lycée ce qu'on appelle "la forme canonique" d'un polynôme du second degré qui permet de voir qu'un tel polynôme admet des racines si et seulement si son discriminant est un carré du corps considéré.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Théorie des anneaux
Merci pour votre réponse. Donc ne pas avoir de racine suffit pour qu'un polynôme soit irréductible d'après la proposition que vous avez énoncé.
Ici le discriminant est , pouvez-vous être plus explicite sur le "carré du corps considéré"?
, pouvez-vous être plus explicite sur le "carré du corps considéré"?
Je vous remercie pour votre temps.
Je suis un peu mélangé car ici nous ne somme pas dans R ou C, mais bien dans Z/5Z
Ici le discriminant est
Je vous remercie pour votre temps.
Je suis un peu mélangé car ici nous ne somme pas dans R ou C, mais bien dans Z/5Z
Re: Théorie des anneaux
Faire attention aussi au fait que ça, c'est LE truc à ne jamais écrire sans préciser (écrit en rouge et souligné 5 fois) que ce n'est vrai QUE pour les polynômes de degré 2 ou 3. Et ça vient tout bêtement du fait que, si un polynôme de degré 2 ou 3 est factorisable, alors il admet forcément (au moins) un facteur de degré 1.MaitreMoulax a écrit:Donc ne pas avoir de racine suffit pour qu'un polynôme soit irréductible d'après la proposition que vous avez énoncé.
Par contre, il est bien clair que c'est complètement faux à partir du degré 4 : X^4+1 est clairement sans racine sur R [car x^4+1>0 pour tout réel x] et il est tout aussi clairement non irréductible dans R vu que la théorie nous dit que seul les polynômes de degré 1 et ceux de degrés 2 à discriminant <0 sont irréductible dans R.
Remarque : On peut aussi le voir sans aucune théorie en constatant que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
