Théorèmes sur les fonctions implicites

[egan]

Bonsoir,

J'étudie actuellement une fonction implicite pour laquelle j'aimerais affirmer ou non la continuité et la dérivabilité. Cependant, le théorème des fonctions implicites ne me permet pas spécialement de conclure comme je le voudrais.
Connaissez-vous des théorèmes plus généraux ou similaires concernant le sujet ?

En vous remerciant par avance.

@+ Boris.

[bentaarito]

c'est quoi le théorème des fonctions implicites que t'as?

A priori la fonction implicite a même régularité que la fonction de départ et ceci au voisinage du point d'inversion ( le théorème est parfois qualifié aussi d'inversion locale )

[egan]

En fait, je pense que c'est juste une petit incompréhension de ma part. Je traite un cas hyper simple pour pas trop m'embêter avec les détails.

Soit f définie sur un ouvert U de dans de classe 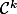, 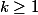. Soit tel que f(a;b)=0 mais tel que .

La version que l'on m'a donné affirme alors que:

- il existe V et W deux intervals ouverts de contenant respectivement a et b et tels que V x W est inclus dans U
- il existe une fonction définie sur V et à valeurs dans W et de classe 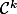telle que:



Cela sous-entend donc que pour pour tout x dans V, il existe un unique y dans W tel que f(x;y)=0.
On est d'accord ?

[bentaarito]

oui correct