Théorème de la limite centrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 21 Mai 2008, 19:38
par aure555 » 21 Mai 2008, 19:38
Bonsoir, voici l'énoncé qui me pose problème :
On considère une suite de variable aléatoire
_{k\geq 1})
qui prennent les valeurs
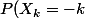 = P(X_k = -k+1) = P(X_k = -k+2) = ... = P(X_k = k-1) = P(X_k = k) = \frac{1}{2k+1})
La question est la suivante : Peut-on appliquer pour cette suite le théorème de la limite centrale?
Je ne voit vraiment pas comment répondre à cette question...
Que doit-on vérifier sur la suite pour pouvoir appliquer ce théorème?
MErci d'avance pour l'aide apportée...
-
mathelot
 par mathelot » 21 Mai 2008, 20:23
par mathelot » 21 Mai 2008, 20:23
Bonjour,
Une condition suffisante du
Grenzwertsatz de Polya, mal traduit par "théorème central limite": les variables sont supposées indépendantes et de même loi.
içi
)
dépend de l'indice k.
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 21 Mai 2008, 21:32
par aure555 » 21 Mai 2008, 21:32
Ok donc c'est parce que, ici , elles ne sont pas de même loi qu'on ne peut appliquer le théorème?
J'avoue avoir beaucoup de mal avec ces notions :triste:
-
mathelot
 par mathelot » 22 Mai 2008, 08:32
par mathelot » 22 Mai 2008, 08:32
bjr,
Les hypothèses du théorème de la limite centrée sont des hypothèses suffisantes mais pas nécéssaires.
aucune de ces hypothèses n'est vérifiées, les variables ne sont pas supposées indépendantes et elles n'ont pas la même loi,ie,
quand on calcule
)
à x fixé, le résultat dépend de l'indice k.
Ce n'est donc pas la même loi pour toutes les variables.
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 22 Mai 2008, 19:08
par aure555 » 22 Mai 2008, 19:08
Bonsoir,
merci pour ton explication.
J'ai un autre énoncé sur le même sujet le voici :
Soient
i\geq1)
une suite de variables aléatoires réelles indépendantes de même densité de probabilité
 = \left{ 1/10 \qquad pour \qquad 0<x<10 \\ 0 \qquad ailleurs)
Peut-on appliquer dans ce cas le théorème de la limite centrale? Justifier votre réponse.
J'aurais répondu alors que, comme nos variables sont indépendantes et de même loi, le théorème peut donc être appliqué.
Mais ça me semble trop "évident" du coup :hum: :marteau:
-
mathelot
 par mathelot » 22 Mai 2008, 19:40
par mathelot » 22 Mai 2008, 19:40
aure555 a écrit:J'aurais répondu alors que, comme nos variables sont indépendantes et de même loi, le théorème peut donc être appliqué.
Mais ça me semble trop "évident" du coup :hum:
si c'est ok. Tu es confronté(e) à un aspect désagréable de la démonstration en Logique,son automaticité, qui fait que, dès que les hypothèses d'un théorème sont vérifiées, la conclusion en découle automatiquement.
c'est en ce sens, que lorsque on dispose de théorèmes très puissants (comme par exemple la classification des groupes ou des variétés en géomètrie), on obtient ensuite de nombreux résultats sans "efforts".

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 22 Mai 2008, 19:42
par nuage » 22 Mai 2008, 19:42
Salut,
On peut appliquer le théorème central limite dans le deuxième cas.
Dans le premier je crois que la moyenne et la somme des
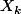
tendent vers une loi normale, mais c'est plus délicat et je peux me tromper.
Ps : j'ai une mauvaise connexion en ce moment. Je vous prie de bien vouloir m'excuser si je ne réponds pas
-
aure555
- Membre Naturel
- Messages: 95
- Enregistré le: 01 Mai 2008, 13:45
-
 par aure555 » 22 Mai 2008, 19:46
par aure555 » 22 Mai 2008, 19:46
D'accord merci beaucoup pour l'aide fournie.
Je sens que je commence à aimer certains aspects de la probabilité :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
