Theoreme de la limite centrale.

[Mathusalem]

Bonjour,
Je suis entrain d'essayer de comprendre la preuve de la limite centrale. Il y a un passage qui m'échappe :
On a des variables normalisées de type quelconque (identiquement distribuées et indépendantes) que l'on nomme .
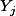
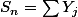
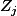
On introduit des variables de loi N(0,1), iid


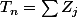
On cherche à comparer .
On me dit que ceci est identique à

Où I est la fonction indicatrice.
Je n'ai pas souvenir de cette propriété dans mon cours.
Quelqu'un peut-il m'expliquer ce passage ?

[Sylviel]

Ouai la transformation de probabilité en espérance d'une indicatrice est un truc archi courant en proba.
Je ne sais même pas comment en faire une "démonstration" tant c'est proche de la définition d'une proba... On va noter mu la mesure de proba, meme si c'est la meme chose que P juste pour que tu voies un peu mieux ce qui se passe

[Mathusalem]

Ouai la transformation de probabilité en espérance d'une indicatrice est un truc archi courant en proba.
Je ne sais même pas comment en faire une "démonstration" tant c'est proche de la définition d'une proba... On va noter mu la mesure de proba, meme si c'est la meme chose que P juste pour que tu voies un peu mieux ce qui se passe

Merci beaucoup.
En effet ça me paraissait intuitif mais j'suis pas bon pour montrer "rigoureusement"

Reste plus qu'à comprendre la preuve !
Bonne soirée