Théorème de green riemann
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bilou51
- Messages: 6
- Enregistré le: 05 Jan 2013, 20:28
-
 par bilou51 » 09 Juin 2013, 15:39
par bilou51 » 09 Juin 2013, 15:39
Bonjour,
Soit D l'ensemble définit par : 0
Je dois trouver l'aire de D avec Green Riemann (=14/3).
A(D) = 1/2 S (4à2) -t-4-t + 1/2 S (2à0) 2t²-4t² (à partir des paramétrisation de chaque morceau de la courbe étudiée).
= 1/2 S (2à4) 2t²-4 + 1/2 S (0à2) 2t² 14/3.
S est le symbole "intégrale"
Dans la correction ils posent P(x,y)=0 et Q(x,y)=x, mais je ne comprends pas, pourquoi, d'où il peuvent faire ça.. Mais ils trouvent 14/3...
Quelqu'un peut-il m'aider ?
Merci d'avance
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Juin 2013, 16:42
par Kikoo <3 Bieber » 09 Juin 2013, 16:42
bilou51 a écrit:Dans la correction ils posent P(x,y)=0 et Q(x,y)=x, mais je ne comprends pas, pourquoi, d'où il peuvent faire ça..
C'est justement la définition du théorème de Green-Riemann !
"Pour un domaine D inclus dans R², fermé, borné et "sympathique" (jonction d'arcs C1, qui font du bord un arc C1 par morceaux), alors avec

"orienté vers la droite", on a :
[CENTER]
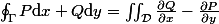 \mathrm{d}x\mathrm{d}y)
[/CENTER]
P et Q viennent d'un champ de vecteurs lui-même sympathique genre
=(P(x,y),Q(x,y))=(0,x))
PS : J'ai parlé trop vite et n'en suis pas venu à l'explication ! Alors ce champ de vecteurs a la particularité de bien se comporter car il te donne du x(t)dy qui est souvent facile à intégrer après un changement de variables polaires par exemple.
-
bilou51
- Messages: 6
- Enregistré le: 05 Jan 2013, 20:28
-
 par bilou51 » 09 Juin 2013, 16:52
par bilou51 » 09 Juin 2013, 16:52
Kikoo <3 Bieber a écrit:C'est justement la définition du théorème de Green-Riemann !
"Pour un domaine D inclus dans R², fermé, borné et "sympathique" (jonction d'arcs C1, qui font du bord un arc C1 par morceaux), alors avec

"orienté vers la droite", on a :
[CENTER]
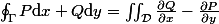 \mathrm{d}x\mathrm{d}y)
[/CENTER]
P et Q viennent d'un champ de vecteurs lui-même sympathique genre
=(P(x,y),Q(x,y))=(0,x))
Oui, d'accord, mais... En cours, on nous a dit d'utiliser et de retenir que la formule
A(D)=1/2 S xdy - ydx.
Pourquoi, là, ça ne fonctionne pas?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 09 Juin 2013, 16:58
par Kikoo <3 Bieber » 09 Juin 2013, 16:58
bilou51 a écrit:Oui, d'accord, mais... En cours, on nous a dit d'utiliser et de retenir que la formule
A(D)=1/2 S xdy - ydx.
Pourquoi, là, ça ne fonctionne pas?
Celui-là marche aussi, ou bien le champ (-y,0)
PS : Enfin ça dépend, parfois un champ sera plus sympathique qu'un autre, et sera plus adapté dans le sens où il t'épargne des calculs plus longs et qui dit calculs longs dit plus de chances de se tromper.
-
bilou51
- Messages: 6
- Enregistré le: 05 Jan 2013, 20:28
-
 par bilou51 » 09 Juin 2013, 17:14
par bilou51 » 09 Juin 2013, 17:14
Kikoo <3 Bieber a écrit:Celui-là marche aussi, ou bien le champ (-y,0)
PS : Enfin ça dépend, parfois un champ sera plus sympathique qu'un autre, et sera plus adapté dans le sens où il t'épargne des calculs plus longs et qui dit calculs longs dit plus de chances de se tromper.
C'est bizarre car je ne trouve pas le bon résultat... :--:
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 19 Juin 2013, 10:08
par deltab » 19 Juin 2013, 10:08
Bonjour.
La formule de Green-Rieman avec les bonnes hypothèses sur \Gamma, P et Q est:
dx+Q(x,y)dy =\iint_D(\dfrac{\partial Q}{\partial x}(x,y)-\dfrac{\partial P}{\partial y}(x,y))dxdy)
Si
-\dfrac{\partial P}{\partial y}(x,y))
est une constante C non nulle, on aura alors:
dx+Q(x,y)dy =\dfrac{1}{C}\iint_D(\dfrac{\partial Q}{\partial x}(x,y)-\dfrac{\partial P}{\partial y}(x,y))dxdy=\iint_D dxdy)
et l'intégrale curviligne
dx+Q(x,y)dy)
sera bien l'aire de D.
C'est le cas quand on prend
=y)
et
=x)
(
-\dfrac{\partial P}{\partial y}(x,y)=2)
) ou encore
=0)
et
=x)
(
-\dfrac{\partial P}{\partial y}(x,y)=1)
).
On pourra s'amuser à trouver des couples de fonctions (P,Q) tels que
-\dfrac{\partial P}{\partial y}(x,y))
soit une constante C non nulle et il y en a même une infinité.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
