Théorème des extremas liés
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 20:56
par nivéa » 27 Aoû 2008, 20:56
Bonsoir,
je n'arrive pas à montrer qu'il y a au plus 8 extrema dans D1
:x^2+y^2=1})
Auriez-vous une piste !!

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 21:13
par leon1789 » 27 Aoû 2008, 21:13
D1 est le disque unité de R^2, c'est ça ?
-
digardel
- Membre Naturel
- Messages: 84
- Enregistré le: 26 Aoû 2008, 15:36
-
 par digardel » 27 Aoû 2008, 21:17
par digardel » 27 Aoû 2008, 21:17
Ta question doit etre incomplète je pense .Des extréma ,ce sont des extrémas d une fonction,obligatoirement
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 21:20
par nivéa » 27 Aoû 2008, 21:20
digardel a écrit:Ta question doit etre incomplète je pense .Des extréma ,ce sont des extrémas d une fonction,obligatoirement
oui, la question exact est: déduire à l'aide du théorème des extrema liés que f (ici f étant une fonction )présente au plus 8 extrema.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 21:21
par nivéa » 27 Aoû 2008, 21:21
leon1789 a écrit:D1 est le disque unité de R^2, c'est ça ?
oui, c'est ça dans IR²

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Aoû 2008, 21:22
par leon1789 » 27 Aoû 2008, 21:22
Tu ne penses pas que nous préciser la fonction f serait utile ?...... :hum:
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 27 Aoû 2008, 21:33
par nivéa » 27 Aoû 2008, 21:33
ouii, pardon ,je pensai l'avoir mises :girl2:
f(x,y)=

 par busard_des_roseaux » 28 Aoû 2008, 07:03
par busard_des_roseaux » 28 Aoû 2008, 07:03
bjr,
1) s'agit-il du cercle ou du disque unité ?
2) passer en coordonnées polaires !
-
digardel
- Membre Naturel
- Messages: 84
- Enregistré le: 26 Aoû 2008, 15:36
-
 par digardel » 28 Aoû 2008, 11:29
par digardel » 28 Aoû 2008, 11:29
çà me parait bizarre ton truc j en trouve que 2 possibles sur le disque unités ,ceci dit 2 c est moins que 8
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Aoû 2008, 13:24
par Doraki » 28 Aoû 2008, 13:24
C'est sur le cercle, pas sur le disque.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 28 Aoû 2008, 18:32
par nivéa » 28 Aoû 2008, 18:32
bonjour, busard des roseaux, vous avez écrit de passer en coordonnées polaires?????
je n'arrive pas trop à saisir l'exercice.
soit la fonction
=x^2+y^2+x^3y^3)
soit
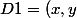:x^2+y^2=1\right)
1)déduire à l'aide du théorème des extrema liés que f présente au plus 8 extrema dans D1.
PS: si ça peut vous aider les solutions des points critiques
)
(
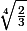
,-
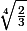
) , (-
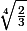
,
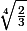
)
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 28 Aoû 2008, 23:17
par nivéa » 28 Aoû 2008, 23:17
comme faire, qui aurai une piste?!!
c'est que je ne sais pas comment m'y prendre pour commencer :triste:
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 28 Aoû 2008, 23:46
par nivéa » 28 Aoû 2008, 23:46
pour commencer il faut poser une condition nécessaire:

soit
=x^2+y^2+x^3y^3)
=>

???
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 29 Aoû 2008, 00:07
par skilveg » 29 Aoû 2008, 00:07
Si je ne m'abuse, quand il y a un extremum, le gradient de

est prependiculaire à la courbe non? Si l'équation de la courbe est
=0)
, ça donnerait l'équation

d'où une majoration du nombre de solutions.
J'espère ne pas trop raconter n'importe quoi...
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 29 Aoû 2008, 00:11
par skilveg » 29 Aoû 2008, 00:11
nivéa a écrit:pour commencer il faut poser une condition nécessaire:

D'ailleurs ça c'est faux: ce serait vrai sur un ouvert, mais là on est sur une courbe. On peut avoir un extremum sans que le gradient s'annule (on a peut-être un "meilleur extremum" un peu plus loin mais à l'extérieur de la courbe).
De mon côté j'aboutis à l'équation

d'où puisqu'on est sur le cercle

. L'intersection de cette hyperbole et du cercle unité comporte au plus quatre points. On a donc au plus quatre extrema sur le cercle, et donc au plus sept sur le disque.
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 29 Aoû 2008, 00:16
par nivéa » 29 Aoû 2008, 00:16
bonsoir,
en fait je ne sais pas trop comment mis prend pour résoudre cet exo, je ne comprend pas très bien l'énonce en lui même!!!
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 29 Aoû 2008, 00:31
par nivéa » 29 Aoû 2008, 00:31
je pense que je me trompe mais je crois que vous vous êtes trompé c'est

au lieu de

-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 29 Aoû 2008, 00:34
par skilveg » 29 Aoû 2008, 00:34
Euh non je ne crois pas, en tout cas pas en caractéristique nulle. En général quand je dérive

il me sort un facteur trois, je n'y peux rien...
-
nivéa
- Membre Relatif
- Messages: 209
- Enregistré le: 19 Aoû 2008, 17:32
-
 par nivéa » 29 Aoû 2008, 00:40
par nivéa » 29 Aoû 2008, 00:40
skilveg a écrit:De mon côté j'aboutis à l'équation

d'où puisqu'on est sur le cercle

. L'intersection de cette hyperbole et du cercle unité comporte au plus quatre points. On a donc au plus quatre extrema sur le cercle, et donc au plus sept sur le disque.
je suis désolée d'insister comme ca mais je n'arrive pas à comprend d'où vient le 3. et cette expression

. :girl2:
-
skilveg
- Membre Relatif
- Messages: 462
- Enregistré le: 21 Mai 2008, 21:29
-
 par skilveg » 29 Aoû 2008, 00:54
par skilveg » 29 Aoû 2008, 00:54
Bon, je reprends les calculs, je me suis peut-être planté après tout...
(Au passage, c'est fou le nombre de Bob l'éponge qu'on peut croiser à ces heures indues :ptdr: )
=x^2+y^2+x^3 y^3)
, donc
=\begin{pmatrix} 2 x+3 x^2 y^3 \\ 2 y+3 x^3 y^2 \end{pmatrix})
.
J'écris la condition que je pense être légitime:
\cdot\begin{pmatrix}{2x}\\{2y}\end{pmatrix}=0)
soit

que je réécris

. D'où la fin.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
d'où puisqu'on est sur le cercle
. L'intersection de cette hyperbole et du cercle unité comporte au plus quatre points. On a donc au plus quatre extrema sur le cercle, et donc au plus sept sur le disque.