Théorème de Beatty !!
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Juin 2008, 18:12
par raito123 » 30 Juin 2008, 18:12
Slt:happy3:,
J'ai du mal à comprendre une relation je voudrais je l'aide si c'est possible !!
On suppose qu'on a

avec

Apparement quand on tend k vers l'infinie on a

Je ne vois pas pourquoi ??
Merci d'avance pour votre aide !! ::):
(A et B deux irrationnel )
Les multiples ne doivent pas être utilisés sans nécessité
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 30 Juin 2008, 18:32
par ThSQ » 30 Juin 2008, 18:32

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Juin 2008, 18:41
par raito123 » 30 Juin 2008, 18:41
Ayeuuh..!!
Pas trop fort avec le marteau :)
C'est bon je pense je savais que c'était la formule qu'il faut utiliser mais je savais pas où !!
Là c'est bon !!
Merci :happy2:!!
Les multiples ne doivent pas être utilisés sans nécessité
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 30 Juin 2008, 18:48
par ThSQ » 30 Juin 2008, 18:48
raito123 a écrit:Pas trop fort avec le marteau

Le marteau c'était pour moi ....

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Juin 2008, 18:49
par raito123 » 30 Juin 2008, 18:49
lol^^
Pk ? c'est la bonne formule !! non ?
Les multiples ne doivent pas être utilisés sans nécessité

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 30 Juin 2008, 18:53
par leon1789 » 30 Juin 2008, 18:53
Amusant ça. Je ne connaissais pas ce résultat.
Tu as des exemples de nombres A,B vérifiant

pour tout

-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 30 Juin 2008, 18:55
par ThSQ » 30 Juin 2008, 18:55
raito123 a écrit:lol^^
Pk ? c'est la bonne formule !! non ?
J'ai dû m'y reprendre à trois fois ....

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 30 Juin 2008, 18:58
par leon1789 » 30 Juin 2008, 18:58
leon1789 a écrit:Amusant ça.
Tu as des exemples de nombres A,B vérifiant

pour tout

La bonne formule est

non ?
(et cela pour tout couple A,B d'irrationnels tels que 1/A+1/B=1)

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Juin 2008, 18:58
par raito123 » 30 Juin 2008, 18:58
Non pas vraiment mais on peut toujours poser la question à Samuel Beatty ou à
Wikipédia
Les multiples ne doivent pas être utilisés sans nécessité

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Juin 2008, 18:59
par raito123 » 30 Juin 2008, 18:59
ThSQ a écrit:J'ai dû m'y reprendre à trois fois ....
Oui j'ai remarquer !^^
Les multiples ne doivent pas être utilisés sans nécessité

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 30 Juin 2008, 19:03
par leon1789 » 30 Juin 2008, 19:03
raito123 a écrit:Non pas vraiment (...)
Tu veux dire que tu n'es pas certain de ton énoncé ? ou bien du mien ?

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Juin 2008, 19:06
par raito123 » 30 Juin 2008, 19:06
D'aprés les sources que j'ai c'est du tiens que je ne suis pas sûr !!!
Jvais voir ça de plus prés ( je veux dire encore plus prés )
Les multiples ne doivent pas être utilisés sans nécessité

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 30 Juin 2008, 19:08
par leon1789 » 30 Juin 2008, 19:08
raito123 a écrit:D'aprés les sources que j'ai c'est du tiens que je ne suis pas sûr !!!
1/A + 1/B = 1 : prendre A,B > 1 ... et alors [1/A] + [1/B] = 0 = 1-1 !

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Juin 2008, 19:14
par raito123 » 30 Juin 2008, 19:14
Non faut prendre en compte les ensembles qui partionnent N* !!
S_A et S_B avec S_A l'ensemble des entiers strictement positive qui s'écrivent sous forme de [nA] pour un certain entier n !!
Si on suppose que S_A et S_B forment une partition de N* alors [k/A] + [k/b] =k ( du fait de la partition)
Les multiples ne doivent pas être utilisés sans nécessité
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Juin 2008, 19:22
par lapras » 30 Juin 2008, 19:22
salut
on suppose que S_A et S_B forment une partition de N*
On n'a même pas a supposer : ce résultat est vrai pour tous irrationnels

et

tels que

on a l'ensemble des valeur prises par
 = [\alpha*n])
et
 = [\beta*n])
forment une partition de

Les hypothèses ne sont pas claires : que supposes tu ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 30 Juin 2008, 19:29
par leon1789 » 30 Juin 2008, 19:29
heu, pardon d'insister, mais malgré un contre-exemple évident, vous continuez à dire [k/a]+[k/b]=k ? ... alors que c'est k-1...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 30 Juin 2008, 19:38
par leon1789 » 30 Juin 2008, 19:38
lapras a écrit:ce résultat est vrai pour tous irrationnels

et

tels que

on a l'ensemble des valeur prises par
 = [\alpha*n])
et
 = [\beta*n])
forment une partition de

...de

? et si
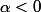
?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 30 Juin 2008, 19:39
par leon1789 » 30 Juin 2008, 19:39
raito123 a écrit:Non (...) [k/A] + [k/b] =k ( du fait de la partition)


le monsieur te dit [k/A] + [k/B] = k-1 ! ...quels que soient

, et

vérifiant 1/A + 1/ B = 1 :++:
-
lapras
- Membre Transcendant
- Messages: 3664
- Enregistré le: 01 Jan 2007, 12:00
-
 par lapras » 30 Juin 2008, 19:41
par lapras » 30 Juin 2008, 19:41
Nous avons

et bien évidemment :

ou

Oui leon tu as raison mais ici on ne sait pas trop ce que raito suppose : suppose, il faut qu'il redonne les hypothèses clairement.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 30 Juin 2008, 19:44
par raito123 » 30 Juin 2008, 19:44
Ce que j'ai poser est vrai pour
aplha et beta deux réel strictement positifs !! et k dans IN*
Les multiples ne doivent pas être utilisés sans nécessité
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités