Théorème de la base normale

[barbu23]

Bonjour à tous : :happy3:
J'aimerai que quelqu'un me propose quelques exemples d'applications du théorème suivant :
si est une extension finie et galoisienne de corps commutatifs , de groupe de Galois , alors il existe tel que l'orbite soit une base du -espace vectoriel .
Par exemple :
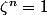
avec : , qui est galoisienne et de groupe de Galois :
Donc, quel est ce tel que : est une base de : - espace vectoriel : ?
Merci d'avance ! :happy3:

[Doraki]

n'importe quel x qui ne soit pas un point fixe d'un élément de G convient.
En l'occurrence, une racine primitive de l'unité.

[barbu23]

Comment tu le sais Doraki ? :happy3:
Merci d'avance ! :happy3:

[yos]

Notation à proscrire. Un isomorphisme, c'est pas une égalité.

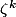
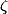
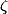
Une base de cette extension doit être formée des où k est premier avec n (racines du polynôme minimal de ). Un élément du groupe de Galois est entièrement déterminé par l'image de qui est l'une des autres racines du polynôme minimal.

[barbu23]

Oui ! Merci beaucoup ! :happy3:

[yos]

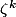
Une base de cette extension doit être formée des où k est premier avec n

Je suis pas sûr de ça en fait. J'y réfléchis.

[Doraki]

Comment tu le sais Doraki ? :happy3:

Parceque si K(G.x) était strictement inclus dans L, ça voudrait dire que K(G.x) est le corps des invariants de L par un sous-groupe H de G, donc que x serait un point fixe de tout un sous-groupe de G.
Donc si on prend x justement point fixe de personne, on est sur d'obtenir L.

[yos]

Parceque si K(G.x) était strictement inclus dans L, ça voudrait dire que K(G.x) est le corps des invariants de L par un sous-groupe H de G, donc que x serait un point fixe de tout un sous-groupe de G.
Donc si on prend x justement point fixe de personne, on est sur d'obtenir L.

Je pense que ton truc est faux : tu confonds l'engendrement linéaire et l'engendrement par opérations de corps.
Je suis d'accord que K(Gx)=L sous ton hypothèse, et d'ailleurs K(x)=L lui aussi, mais ça ne signifie pas que G.x est une base.

[Doraki]

Oui, je me suis rendu compte que (i,-i) ça faisait pas une base de C comme R-ev. Il faut montrer qu'il y a des familles G.x qui sont libres.

Si il y a une liaison, on a que somme des ag*(g.x) = 0 où ag est dans K.
Pour tout g' on peut faire agir g' dessus, ça nous dit que ag.(g'g.x) = 0.
En sommant ça pour tout g', ça nous dit que (somme des ag)(somme des g.x) = 0.

Donc si on a x qui n'est point fixe d'aucun g, ET tel que la somme des g.x est non nulle, on est ptetre un peu mieux parti pour avoir une base.