Soit :
Soit
Soit
On note :
On note pour :
et :
Montrer que :
Voiçi ce que j'ai fait : :happy3:
Soit :
Alors :
avec :
Après, je ne sais pas quoi faire ! :happy3:
Merci d'avance de votre aide ! :happy3:
Théorème de la base adaptée
11 messages
- Page 1 sur 1
Théorème de la base adaptée
par barbu23 » 07 Fév 2010, 16:22
Bonjour à tous :
Soit :
un anneau.
Soit
un - module.
Soit $)
une base de : .
On note : $)
.
On note pour :
:
et :
 = \{ \ f(x) \ / \ f \in M^{*} \ \} $$)
Montrer que :
 \ \ $)
 = c A \ \ \Longleftrightarrow \ \ c = \mathrm{pgcd}(x_{1},...,x_{n}) $)
.
 \ \ $)
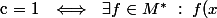 = 1 \ \ \Longleftrightarrow \ \ x \neq 0 \ \wedge \ Ax \text{ a un supplementaire dans } M \ \ \\ \Longleftrightarrow \ \ x \text{ peut etre complete en une base de } M $)
.
Voiçi ce que j'ai fait : :happy3:
Soit : = c.A $)
.
Alors :
tel que :  = f(\displaystyle \sum_{i=1}^{n} x_{i} e_{i}) = \displaystyle \sum_{i=1}^{n} x_{i} f(e_{i}) = \mathrm{pgcd}(x_{1},...,x_{n}) \displaystyle \sum_{i=1}^{n} \frac{x_{i}}{\mathrm{pgcd}(x_{1},...,x_{n})} f(e_{i}) $)
.
avec : | x_{i} $)
pour tout : 
Après, je ne sais pas quoi faire ! :happy3:
Merci d'avance de votre aide ! :happy3:
Soit :
Soit
Soit
On note :
On note pour :
et :
Montrer que :
Voiçi ce que j'ai fait : :happy3:
Soit :
Alors :
avec :
Après, je ne sais pas quoi faire ! :happy3:
Merci d'avance de votre aide ! :happy3:
par yos » 07 Fév 2010, 16:55
La question est mal posée je pense : il s'agit pas d'établir une équivalence, mais de montrer que C(x)=cA où l'on a posé )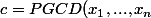
.
Pour faire ça tu fais la double-inclusion :
\subset cA)
est évident.
L'inclusion inverse se fait avec une relation de Bezout sur les
(ce qui m'amène à te demander ce que tu supposes sur l'anneau A : principal m'irait bien).
Pour faire ça tu fais la double-inclusion :
L'inclusion inverse se fait avec une relation de Bezout sur les
par Ben314 » 07 Fév 2010, 16:59
Je rajouterais aussi que d'écrire que M est un A module libre me semblerais aussi assez utile... (pour qu'il ait une base !!!)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par barbu23 » 07 Fév 2010, 19:08
Oui, est un anneau principal ! :happy3:
Pour l'inclusion inverse :
Soit : $)
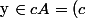alors :  $)
D'après bezout :
On pose : $)
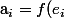Par conséquent :
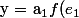 + ... + a_{n} f(e_{n}) = f(a_{1} e_{1} + ... + a_{n} e_{n} )= f(x) $)
Par conséquent :
 $)
( D'où l'inslusion inverse ! :happy3: )
Maintenant, supposons que : = (c) $)
Montrer que : $)
Merci d'avance ! :happy3:
Pour l'inclusion inverse :
Soit :
D'après bezout :
On pose :
Par conséquent :
Par conséquent :
Maintenant, supposons que :
Montrer que :
Merci d'avance ! :happy3:
par barbu23 » 07 Fév 2010, 19:24
Pour la reciporque, voiçi une idée : :happy3:
Supposons que :
 = (c) $$)
On peut ecrire :
 = \{f(x) \ / \ f \in M^{*} \} = \{ x_{1} f(e_{1}) + ... + x_{n} f(e_{n}) \ / \ (f(e_{1}),...,f(e_{n}) ) \in A \ \} \\ = \{ f(e_{1}) e_{1}^{*}(x) + ... + f(e_{n}) e_{n}^{*}(x) \ / \ (f(e_{1}),...,f(e_{n}) ) \in A \ \} \\ = A e_{1}^{*}(x) + ... + A e_{n}^{*}(x) = (e_{1}^{*}(x)) + ... + (e_{1}^{*}(x)) \\ = ( \mathrm{pgcd}(e_{1}^{*}(x), ... ,e_{1}^{*}(x)) ) = ( \mathrm{pgcd}(x_{1} , ... , x_{n})) $$)
Par conséquent : $)
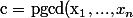! :happy3:
Supposons que :
On peut ecrire :
Par conséquent :
par barbu23 » 07 Fév 2010, 19:29
Comment faire pour la seconde question ? :happy3:
Merci d'avance ! :happy3:
Merci d'avance ! :happy3:
par barbu23 » 07 Fév 2010, 19:47
Pour  $)
: :happy3:
Pour la première équivalence :
 = A $)
On peut voir :
Soit :
tel que :  : M^{*} \longrightarrow A $)
avec : (f) = f(x) = C(x)(f) $)
.
Est ce que : pour
fixé dans :  $)
est surjective pour pouvoir conclure ? :happy3:
Merci d'avance ! :happy3:
Pour la première équivalence :
On peut voir :
Soit :
Est ce que : pour
Merci d'avance ! :happy3:
par barbu23 » 07 Fév 2010, 20:01
Oui, mais par hypothèse :
 = A $)
, par consequent :  = \tau (x) $)
est surjective, donc, pour : 
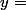
, il existe 
, tel que : (f) = 1 $)
, c'est à dire  = 1 $)
!
On fait comment maintenant, pour la seconde équivalence ?
Merci d'avance ! :happy3:
On fait comment maintenant, pour la seconde équivalence ?
Merci d'avance ! :happy3:
par barbu23 » 07 Fév 2010, 20:01
Pour la seconde equivalence :
 = 0 \neq 1 $)
Par conséquent :
 = 1 $)
Comment faire pour la suite ? :happy3:
Merci d'avance ! :happy3:
Par conséquent :
Comment faire pour la suite ? :happy3:
Merci d'avance ! :happy3:
par barbu23 » 07 Fév 2010, 21:01
svp, un petit coup de main pour la suite ? :happy3:
Merci d'avance ! :happy3:
Merci d'avance ! :happy3:
par barbu23 » 07 Fév 2010, 21:39
Pour l'autre équivalence : :happy3:
On a :
avec 
( 
est un hyperplan de )
Après, qu'est ce qu'on fait ? :happy3:
svp, Aidez moi ! :happy3:
On a :
Après, qu'est ce qu'on fait ? :happy3:
svp, Aidez moi ! :happy3:
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :