Théorème ambigu sur les suites

[Anonyme]

Salut,


Mon problème est simple. En effet, dans mon cours sur les suites, un théorème qui n'est pas dans mon bouquin non plus m 'est apparu ambigu.

Au départ , on m'énonce le théorème que voici : si Un CV vers l appartenant a IR, alors toute sous suite CV vers l et l'application pratique qu'on en fait, c'est que pour montrer qu'une suite est Divergente, on cherche deux suites extraites ayant des limites differentes.


Or y a une autre proposition apres qui dit: si U2n, U2N+1, U3n Convergent, alors Un converge. Pour moi, cela ne peut pas etre vrai car si on a au moins 2 suites dans les trois precedentes qui ne convergent pas vers la même limite, alors d'apres le premier theoreme , Un ne peut pas etre convergente!

Mon theoreme est il faut, l'ai je bien pris en note? Si non Pouvez vous me le reformuler?

merci d'avance:)

[LN1]

Non cette propriété est bien juste

si converge vers L alors aussi car c'est une sous suite de la précédente
si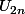 converge vers L' alors aussi (pour les même raison)
ce qui assure que L = L'

Raisonnement analogue en créant une sous suite commune à et

le fait que deux sous-suites aient une infinité de terme en commun les oblige à converger vers la même limite

Enfin si et convergent vers la même limite, la suite (U) converge