Bonjour je suis un étudiant en informatique, j'aimerai effectuer un test de primalité sur des nombres composé de 200 chiffres environ.
Dans mon post N voudra dire le nombre testé il sera forcément impair.
Un test de primalité permet de dire si un nombre est premier ou pas.
Il y a plusieurs façon de procéder pour vérifier si un nombre est premier ou pas en informatique.
On fait une boucle avec un modulo dedans mais bon comprenez que je ne vais pas faire une boucle de 2 jusqu'à un nombre composé de 200 chiffres on ferai aller un processeur peut-être pour rien au final juste pour tester un nombre.
Bon ensuite il y a une technique qui consiste à faire la racine carré de N et de tester tous les nombres premier inférieur à racine de N sur N bon déjà faut connaitre ses antécédents ça nous donne toujours une boucle immense.
Ensuite j'ai trouvé un test Solovay-Strallen qui dit soit un nombre premier A^((N -1)/2) mod(N)= 1 alors N est premier mais bon faire une puissance d'un nombre composé de 200 chiffres est très très long encore une fois. Donc je voulais vous demander un algorithme ou un théorème qui permet de définir si N est premier ou non et cela sans être dans dans gigantesques calculs longs.
Je vous remercie de l'attention que vous porterai à ce post. Cela me permettra de faire un programme qui crypte les messages.
Test de primalité
5 messages
- Page 1 sur 1
bonsoir,
Non, c'est très rapide : pour calculer , tu utilise le fait que :
, tu utilise le fait que :
^2\ \ \ \ \ \ \ \ \ \text{ si } n \text{ est pair}\cr x\big(x^{(n-1)/2}\big)^2\text{ si } n \text{ est impair} \geq 3)
Si est de l'ordre de
est de l'ordre de 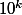 , ça te demande (au pire) de faire
, ça te demande (au pire) de faire }{\ln(2)}k) multiplications pour avoir
multiplications pour avoir  (donc moins de 2000 si n est au environ de
(donc moins de 2000 si n est au environ de 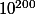 )
)
kangourex a écrit:... mais bon faire une puissance d'un nombre composé de 200 chiffres est très très long encore une fois.
Non, c'est très rapide : pour calculer
Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
