Taylor-Lagrange via Rolle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 16 Mai 2010, 13:55
par AceVentura » 16 Mai 2010, 13:55
Bonjour,
j'essaye de refaire la démonstration de l'égalité de Taylor-Lagrange via le théorème de Rolle. L'idée c'est de définir le réel

par l'égalité
=f(a)+\sum_{k=1}^n\frac{f^{(k)}(a)}{k!}(b-a)^k+\frac{A}{(n+1)!}(b-a)^{n+1})
et de montrer qu'en fait il existe
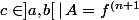}(c))
. Pour cela, on définit la fonction
=f(b)-f(t)-\sum_{k=1}^n\frac{f^{(k)}(t)}{k!}(b-t)^k-\frac{A}{(n+1)!}(b-t)^{n+1})
. Elle est continue sur [a,b], dérivable sur ]a,b[ et
=\varphi(b))
: donc Rolle !
Il faut prouver que
=\frac{(b-t)^n}{n!}(A-f^{(n+1)}(t)))
et c'est ici que je bloque :s
=-f'(t)-\left(\sum_{k=1}^n\frac{f^{(k+1)}(t)}{k!}(b-t)^k-\frac{f^{(k)}(t)}{(k-1)!}(b-t)^{k-1}\right)+\frac{A}{n!}(b-t)^{n})
C'est la grosse parenthèse qui me bloque :/
Merci par avance !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Mai 2010, 14:26
par Ben314 » 16 Mai 2010, 14:26
Ta "grosse somme", coupe là en deux et fait un changement d'indice (de 1) sur une des deux sommes obtenue et OH, MIRACLE... (en fait, c'est un pour fait pour...)
Autre solution (un peu pour les nuls mais à laquelle il faut toujours penser) : au lieu du symbole "sigma", écrit les 3 ou 4 premiers terme pour voir "comment ça marche"...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 16 Mai 2010, 14:34
par AceVentura » 16 Mai 2010, 14:34
=-f'(t)-\sum_{k=1}^n\frac{f^{(k+1)}(t)}{k!}(b-t)^k-\sum_{k=1}^n\frac{f^{(k)}(t)}{(k-1)!}(b-t)^{k-1}+\frac{A}{n!}(b-t)^{n})
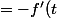-\sum_{k=1}^n\frac{f^{(k+1)}(t)}{k!}(b-t)^k+\sum_{k=0}^{n-1}\frac{f^{(k+1)}(t)}{k!}(b-t)^{k}+\frac{A}{n!}(b-t)^{n})
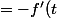-\frac{f^{(n+1)}(t)}{n!}(b-t)^n+f'(t)+\frac{A}{n!}(b-t)^{n}=\frac{(b-t)^n}{n!}(A-f^{(n+1)}(t)))
. MERCI !
J'étais persuadé qu'il fallait ré-indéxer dès lors que l'on dérive, surement des restes du chapitre sur les séries entières :hein:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Mai 2010, 14:40
par Ben314 » 16 Mai 2010, 14:40
Un conseil de "vieux" : à chaque fois qu'une somme te rend un peu perplexe, écrit les 3 ou 4 premiers termes...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
AceVentura
- Membre Relatif
- Messages: 254
- Enregistré le: 04 Mar 2010, 13:46
-
 par AceVentura » 16 Mai 2010, 15:37
par AceVentura » 16 Mai 2010, 15:37
Merci du conseil vieux :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités