Tangentes à une Cardioide

[Pythix]

Bonjour, voici mon problème :
on considère la cardioide C d'équation ;)=1+cos(;))
après l'étude je dois montrer que C admet 3 tangentes dirigées par un même vecteur (non nul).

je pensais résonner avec l'angle de la tangente : tan(v)=;)/;)'
ce qui nous donne v = ;)/2 - pi/2 + kpi
mais après je vois plus trop...

Merci d'avance

[Quidam]

J'appelle 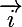et 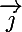les vecteurs unitaires du repère, respectivement sur Ox et Oy, le vecteur unitaire de la droite OM tel que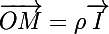
L'angle v dont tu parles, celui dont la tangente est égale à , c'est l'angle si est tangent à la cardioïde (dans le bon sens !)
Si tu veux que la tangente soit parallèle à une direction donnée par un vecteur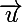 , par exemple, il faut évaluer l'angle et d'après Chasles, .

Si l'on pose , ta condition se traduit par :

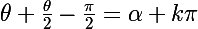
Je te laisse terminer !

[Pythix]

oui je trouve
faut il prendre différentes valeurs de k? trouver une périodicité?
et pour ?

parce que je voulais prendre k=-1 k=0 et k=1 par exemple mais ca pose problème avec l'intervalle, non ?

[Quidam]

De tu peux déduire

trouver une périodicité?

Observe déjà la périodicité de ta courbe ! Dans quel intervalle dois-tu faire varier pour obtenir tous les points de la cardioïde une et une seule fois.
Et ensuite chercher les dans cet intervalle, qui vérifient l'égalité trouvée ci-dessus !

[alben]

Bonjour,
Il te faut exprimer théta en fonction de alpha.
Oui, tu ne peux pas choisir k sans fixer alpha. En revanche pour un alpha donné, tu peux montrer qu'il existe exactement 3 valeurs de k qui donnent un théta tombant dans l'intervalle de définition de la cardioide ..., c'est dire 3 points distincts, ni plus ni moins

[Pythix]

la courbe est décrite entièrement et une seule fois sur un intervalle de longueur 2pi!

je trouve en fixant alpha entre 0 et 2pi comme valeurs de k -2,-1,0,1,2 ...