Bonjour, voici l'énoncé :
Soit f: )
une fonction dérivable et a 
int Dom f. Donnez une équation cartésienne de la tangente au graphe de f au point (a,f(a)). Donnez les coordonnées du point d'intersection entre cette tangente et l'axe des x. Expliquez votre démarche.
L'equation cartésienne est y = f(a) +
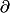
f(a) (x-a)
Pour trouver l'intersection entre cette tangente et l'axe des x, j'annule y...
Donc f(a) +
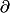
f(a) (x-a) = 0. Ensuite j'isole le x pour avoir l'abscisse...
J'obtiens x = a -
}{\partial f(a)})
Conclusion : les coordonnées du point d'intersection entre cette tangente et l'axe des x est (a -
, 0).
Montrez que o(x^3) = o(x^7))
quand x
0.Rappelez les définitions que vous utilisez et détaillez vos calculs.
Donc une fonction f un est o(
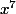
) ssi
}{x^7} \rightarrow 0)
lorsque x
0.
Ensuite pour la preuve je pose f1 la fonction qui est un o(
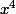
) et f2 = o(
).
Il faut prouver
0 et je décompose
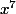
en produit de
ainsi chaque partie tends vers 0 et le total tends vers 0
J'aimerai savoir si tout celà est juste
Merci pour votre aide
