Tangente à un cercle

[Jean16]

Bonjour à tous,
J'ai un dm en mathématique dont je n'arrive pas à résoudre j'aurais donc besoin de votre aide. Voici l'exo :
On considère un point A de coordonnées ( a,0) et un cercle C passant par A de centre P( x(0), y(0) )
1) Ecrire équation de C : (x-x(0))^2+(y-y(0))^2= (x(0)-a)^2 + y(0)^2

2) On considère une droite passant par 0 d'équation y = mx. Ecrire une condition nécessaire et suffisante portant sur m pour que cette droite soit tangente à C.
Pour cette question j'ai écrit que la distance du centre à la tangente au cercle doit être égale au rayon. Mais cela me mène a rien enfin je sais pas quoi faire avec.

3)Trouver une condition nécessaire et suffisante portant sur m et m' pour les que les droites y = mx et y=m'x soient orthogonales.En déduire l'ensemble des points P tels que les deux tangentes à C passant par O soient orthogonales.
Pour cette question j'ai exprimé les vecteurs directeur des deux droites et dit qu'il doivent être orthogonaux ( leur produit scalaire doit être nul) mais cela me mène à rien également.
Si quelqu'un pourrait m'éclaircir ! Merci !

[Pythales]

1) est exact
2) La méthode est bonne. Je ne vois pas pourquoi tu n'aboutis pas. Remarque que le problème n'a pas toujours de solutions, du moins réelles.
3) En réfléchissant, tu dois trouver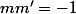 (résultat classique)
La courbe qu'on te demande de déterminer s'appelle courbe orthoptique. Dans le cas présent, tu dois trouver un cercle

[Ericovitchi]

Pour 2) tu peux aussi couper ton cercle avec y=mx en remplaçant y par mx dans ton équation de cercle. Et puis tu dis qu'il faut que le discriminant soit nul pour que les droites soient tangentes. C'est plus sympa que de passer par des distances.

[Jean16]

pour la question 2 : en fait je n'arrive pas à simplifier le gros bloc que j'ai et trouver des solution pour m
la question 3 : je trouve bien mm'=-1. Pour l'ensemble des points P je vois pas...

[Black Jack]

Si je ne m'abuse :

La distance entre un point P(k,l) et une droite d'équation: Ax + By + C = 0 est : d = |Ak+Bl+C|/V(A²+B²) (avec V pour racine carrée).

Et dans le cas de l'exercice : A = -m, B = 1 , C = 0, k = Xo et l = Yo

Il suffit ensuite d'exprimer que d² = R² (avec R le rayon du cercle).

Tu devrais arriver à une équation du second degré en m, dont les 2 solutions réelles (si elles existent) donnent les 2 valeurs (en fonction de Xo,Yo et de a) de m qui conviennent.

:zen:

[Jean16]

ok merci je vais essayé.

[Pythales]

Je me suis trop avancé avec la courbe orthoptique. Je n'avais pas réalisé que c'était le cercle qui bougeait.
En faisant une figure, tu vois que le rapport des distances du centre du cercle au point O et au point A vaut . Le centre décrit bien un cercle (centré sur Ox), mais ce n'est pas le cercle orthoptique.

[Jean16]

Bonsoir,
j'ai bien une équation du second degré mais c'est énorme ce que j'ai pour le delta... encore pire pour les deux solutions .
Pour delta = 4(Xo)^2(Yo)^2-4(-1-(Xo)^2)((Xo)^2+a^2-2(Xo)a-1).
ça me parait assez bizarre...
Merci pou votre aide.

[Ben314]

Salut,
Je sais pas comment tu as mené les calculs, mais ça m'a l'air d'être du "Lourd".

La distance de la droite d'équation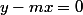 au point est donc la droite est tangente au cercle si et seulement si où est le rayon du cercle.
Concernant la question 2), "Ecrire une condition nécessaire et suffisante portant sur m pour que cette droite soit tangente à C." ben... on vient de répondre à la question.

Aprés, pour la question 3), aprés avoir vu que les droites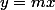 et sont orthogonales ssi 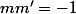, ben faut un peu simplifier l'équation (mais on ne te demande nulle part de la résoudre !!!!)

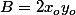où ; et
et là, on te demande à quelle conditions les deux racines et 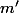de cette équation vérifient elles ?
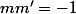Peut être te souvient tu d'un truc concernant le produit des racines d'une équation du second degrés...

Remarque : si alors est forcément positif...

[Jean16]

Merci . je pense avoir trouvé enfin ce qu'il restait à trouver.
Les position du point P est un cercle de centre O et de rayon sqrt(2)*r ?
Merci beaucoup !

[Ben314]

Merci . je pense avoir trouvé enfin ce qu'il restait à trouver.
Les position du point P est un cercle de centre O et de rayon sqrt(2)*r ?
Merci beaucoup !

Non, ce n'est pas tout à fait ça car le rayon r dépend lui même de la position du point P.
En fait, c'est l'inconvéniant d'avoir donné un nom à ce rayon : il ne faut pas oublier durant tout les caculs que r dépend de xo, yo et de a (l'avantage étant bien sûr que toutes les formules sont beaucoup plus courtes à écrire)

[Jean16]

Exact j'ai pas fait attention. Merci beaucoup !