Systèmes linéaires - Déterminant

par **benekire2** » 06 Oct 2010, 18:01

Bonsoir,

Aujourd'hui en cours , la prof m'a parlé des systèmes linéaires et plus particulièrement des systèmes de Cramer. Elle m'a dit de me renseigner sur le sujet , dont j'ignore tout, et elle m'a dit de regarder la définition du déterminant - assez horrible je dois avouer , même si par le pivot de gaus ça se calcule vite et bien dans beaucoup de cas - et je peine sur un exo :

Cela concerne les matrices par blocs. Soit A,B des matrices carrés de taille n. Il me faut montrer que

Merci de votre aide !

par **Skullkid** » 06 Oct 2010, 18:38

Essaye en faisant des opérations sur les lignes et les colonnes.

par **Nightmare** » 06 Oct 2010, 18:52

Généralisation au calcul de

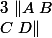
(avec disons A et C qui commutent) ?

par **benekire2** » 06 Oct 2010, 21:19

Salut,

J'aimerais bien rendre cette matrice triangulaire et pouvoir calculer facilement sont déterminant, mais le problème c'est que je vois pas comment m'y prendre techniquement sur les opérations a faire. J'ai l'impression qu'en voulant "éliminer" le B en bas a gauche on modifie totalement la tête du A en bas a droite.

par **Ben314** » 06 Oct 2010, 21:53

benekire2 a écrit:...J'ai l'impression qu'en voulant "éliminer" le B en bas a gauche on modifie totalement la tête du A en bas a droite...

Ce qui est assez normal vu que le résultat que tu doit trouver n'est pas de la forme det(A)x?...

Indic : Ca donne quoi si aux lignes de n+1 à 2n tu ajoute respectivement les lignes 1 à n (ce qui ne change évidement pas le determinant) ?

par **benekire2** » 06 Oct 2010, 22:02

Salut,

Ca fait qu'on se retrouve avec la matrice (A B // A+B A+B) et il suffit de soustraire les colones ^^ :zen: Merci !!

Par contre j'ai trouvé une réécriture miraculeuse : (AB//BA)(A0//-B I)=(A²-B² B//0 A)

..

par **Ben314** » 06 Oct 2010, 22:35

ATTENTION : la multiplication matricielle N'EST PAS COMMUTATIVE...
(donc j'ai de gros doute sur le 0 en bas à droite de ton résultat dans le cas où A et B ne commutent pas...)

Par contre (I 0//I I)(A B//B A)(I 0//-I I) se simplifie, mais c'est la même chose que de faire des opérations sur les lignes/colonnes...

par **benekire2** » 07 Oct 2010, 09:02

Oui je sais elle n'est pas commutative, mais je vois pas où j'ai effectué de multiplication ? J'ai ajouté les ligne 1 a n aux lignes n+1 a 2n puis soustrait les colones n+1 a 2n aux colones 1 a n.

Sinon, j'ai un petit calcul de déterminant :

En développant par rapport a la première ligne, j'obtiens (b+c)²(c+a)²(a+b)²-(b+c)²b²c²-a²b²(a+b)²-a²c²(c+a)²+2a²b²c

Le problème c'est que c'est assez affreux, y a pas mieux pour calculer ce déterminant ?

Merci ,

par **Ben314** » 07 Oct 2010, 16:12

benekire2 a écrit:Oui je sais elle n'est pas commutative, mais je vois pas où j'ai effectué de multiplication ?..

Comment as tu fait ce calcul :

benekire2 a écrit: (AB//BA)(A0//-B I)=(A²-B² B//0 A)

benekire2 a écrit:Sinon, j'ai un petit calcul de déterminant :

Sur les calculs de déterminants, il faut TOUJOURS priviligier les simplifications par combinaisons linéaires au développement par rapport à une ligne/colonne (priviligier la réflexion par rapport à l'automatisme).
Par exemple, si tu retranche la ligne 1 aux lignes 2 et 3 il apparait immédiatement deux facteurs...

par **benekire2** » 07 Oct 2010, 17:36

Salut ben !

A oui, pour la deuxième "preuve" je vois mieux ... pour avoir forcément BA-AB=0 faut que A et B commutent.
et puis effectivement, sur l'écriture que tu m'a donné sous forme de produit de matrice, comme ce sont les matrices associées aux opérations élémentaires ça ne change rien ..

Sinon en effet il m'as été conseillé d'utiliser le pivot de Gauss plutôt que de développer par les lignes et colonnes ... et merci pour le "truc" , je vais en calculer deux trois dans le genre,

Merci ,

par **Sylviel** » 07 Oct 2010, 17:44

quand tu te seras un peu entraîné aux calculs basiques de déterminants j'en ai quelques uns plutôt sympatiques en réserve...

par **benekire2** » 07 Oct 2010, 17:45

Je te fais confiance pour ça sylviel (un moment que je t'avais pas croisé ! Bonjour :id: ).... au passage je viens de voir le déterminant de Vandermonde ... pas trop mal :zen: ils sont dans le genre ?

Pose les et je les ferrais petit a petit ! (dès que je me serais "assez" entraîner avec les basiques)

par **Sylviel** » 07 Oct 2010, 17:53

grumpf, j'ai la flemme de faire du LaTeX. Je t'en pose un que je trouve sublime...
a b b ... b
c a b ... b
c c a ... b
...
c ... a

en clair : des a sur la diagonale, des b dans le coin en haut à droite, des c en bas à gauche.

La méthode de résoution que je préfère consiste à considérer le même déterminant "en ajoutant un x à chaque nombre"...

par **benekire2** » 07 Oct 2010, 18:03

D'accord ... ça me parait pas super simple tout ça ... Mais je soit c'est par réccurence , j'essaierais , soit c'est par développement soit par Gauss soit par ... les trois.

Mais bon, tu conseille d'introduire un x de dans , enfin de l'ajouter de partout, on trouve donc un déterminant polynôme en x et on verra ce que l'on en tire, s'il est de degré faible c'est génial et si on arrive a le déterminer on prendra sa valeur pour x=0 , ce ne sont que des suppositions, j'ai fais très peu de calculs. Je te dit quand j'ai un problème.

par **benekire2** » 08 Oct 2010, 08:39

Bonjour,

J'ai une question en outre , on travaille généralement dans un corps et une matrice est inversibole ssi son déterminant est non nul. Cela dit si on considère l'ensemble des matrices a coefficients dans un anneau , genre dans Z , comment montrer que une matrice est inversible ssi son déterminant est inversible dans cet anneau ? Parce que j'ai vu l'expression théorique d'une matrice inversible, 1/det * t com avec t com la transposée de la comatrice associée a la matrice en question. Faudrait donc que le déterminant divise la comatrice , ou alors que le déterminant soit inversible , mais je vois pas comment montrer que forcément le déterminant doit être inversible ...

Merci !

par **Nightmare** » 08 Oct 2010, 08:51

Salut,

il n'y a pas de problème, comme tu l'as dit, si le déterminant de ta matrice A est inversible on peut définir son inverse par

(attention, c'est la transposée de la comatrice.)

Réciproquement s'il existe B telle que AB=BA=Id il est clair que le déterminant est de A doit est inversible.

par **Nightmare** » 08 Oct 2010, 08:56

Au fait, quel sens donnes-tu à "le déterminant divise la comatrice" ?

par **benekire2** » 08 Oct 2010, 09:00

Salut nightmare :lol3:

J'avais édité mon message pour la transposée.

Pour le sens de "diviser la comatrice" c'était vite dit , c'est "le déterminant divise tout les coefficients de la matrice de manière a ce que un coeff a de notre matrice s'écrive det*b avec b dans notre anneau bien sûr" et c'est nécéssaire si on suppose le déterminant de la matrice non inversible.

Par contre je vois pas trop comment tu conclu :"Réciproquement s'il existe B telle que AB=BA=Id il est clair que le déterminant est de A doit est inversible."

C'est précisément ce que je veut montrer .. et ça ne me parrait pas hyper évident. Je pense qu'il faut bidouiller avec l'expression de la comatrice.

par **Nightmare** » 08 Oct 2010, 09:04

ben il suffit de passer au déterminant :

det(A)det(B)=det(B)det(A)=1 ce qui veut bien dire que det(A) est inversible d'inverse det(B).

par **benekire2** » 08 Oct 2010, 09:09

A oui en effet cela ne m'étais même pas vennu à l'esprit. Donc inutile de bidouiller avec les coefficients de la comatrice ..

Sinon, une question en rapport , y a-il toute une théorie sur les matrices, déterminants dans des anneaux ? Ou alors ce n'est "pas la peine" car il y a très peu de résultats qui changent ? De même souvent, les coprs de base sur le peu que j'ai vu d'algèbre linéaire sont R ou C , et certains résultats ( la plupart je pense) se généralisent a un coprs quelconque, alors est-ce que il existe aussi toute une théorie autour de l'algèbre linéaire sur "tout coprs" en fin je veut dire sur des coprs qui ne sont pas forcément R ou C ... ? je suppose que oui pour cette question ...

Systèmes linéaires - Déterminant

Systèmes linéaires - Déterminant

Qui est en ligne