Bonjour,
pouvez vous me dire si je ne me trompe pas?
Soit la matrice d'un système:
1 0 0 3
0 1 0 2
0 0 1 1
0 0 0 1
1) De combien de variables le système est il composé?
2) De combien d'équations le système est il composé?
3) Quel est le rang de la matrice?
4) Qu'en déduire concernant la solution?
Je dirais:
1) 4 variables (ou 3? je ne sais pas si la dernière colonne est une variable ou un terme indépendant....?)
2) 4 équations
3) rang= 4
4) ?
Merci d'avance!
Systèmes d'équations (matrices)
4 messages
- Page 1 sur 1
Non ça ne suffit pas : le rang de la matrice 2x2 avec des 1 partout est de 1 alors que la diagonale est bien composée uniquement de chiffres 1.
Pour que le rang soit égal à 4, dans ton cas, il suffit de dire que la matrice est triangulaire supérieure de coeffiscients diagonnaux non-nuls. (ce qui revient à dire que les lignes ou colonnes forment une base de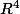 )
)
Pour que le rang soit égal à 4, dans ton cas, il suffit de dire que la matrice est triangulaire supérieure de coeffiscients diagonnaux non-nuls. (ce qui revient à dire que les lignes ou colonnes forment une base de
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
