Systèmes différentiels

[fresnilla]

bonsoir,

J'aimerai savoir quelles sont les étapes permettant de résoudre un système différentiel diagonalisable ?

comme celui ci par exemple
(x'1) = 4.(x1) + 3.(x2) + (x3)
(x'2) = 23.(x1) + 12.(x2) + 3.(x3)
(x'3) = -99.(x1) - 57.(x2) -16.(x3)

merci !

[fresnilla]

merci hatake51 pour ta réponse,
justement j'avais fait cela mais ma réponse s'est avérée fausse.

dans l'énoncé on a
" Une base des solutions est de la forme e^(a1*t)*V1, e^(a2*t)*V2, e^(a3*t)*V3. Calculer les ai et les vecteurs Vi correspondants "

j'ai alors pris la matrice :
4 3 1
23 12 3
-99 -57 -16

et j'ai caculée les valeurs propres que voici : -2 , -1 et 3
les vecteurs propres correspondants (dans le même ordre) sont (1, -1, -3) , (1, -2, 1) et (0, 1, -3)


quelle est donc la bonne réponse ?

merci encore !

[Maxmau]

Bj
Les ai sont les vp (valeurs propres). Les Vi sont les VP

[fresnilla]

j'ai compris cela Maxmau, mais je ne sais comment trouver les bonnes réponses.

voici l'exo

j'ai beau chercher mais ... :triste:

[Maxmau]

Je n'ai pas vérifié tes calculs. Je prends tes résultats.
Tu entres a1 = -2 puis V1 = (1 , -1 , -3) ...etc...

[Mathusalem]

La matrice des vecteurs propres te donne ta matrice de passage dans la base de vecteurs propres.
On la nomme P
On nomme la matrice differentielle M
Donc tu as que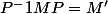
M' etant ta matrice diagonalisee. En general tu n'es pas oblige de passer par ce calcul, tu peux simplement mettre dans l'ordre les valeurs propres associees aux vecteurs propres sur ta diagonale
p. ex
1 0 0
0 -2 0
0 0 3
J'ai pas tes valeurs en tete, desole.
Toujours est-il que tu auras que M' est diagonalisee avec les valeurs que tu as.
Donc tu peux resoudre maintenant tres facilement les equations differentielles.. Mais celles-ci te donne (si tes fonctions sont f g et h) les resultats de f' g' h' car tu es dans la base propre.

Donc une fois que tu as tes resultats, il te faut repasser dans la base normale avec la matrice inverse.

[fresnilla]

merciiiii à tous ceux qui m'ont aidé !

je l'ai enfin résolu grâce à votre aide

bonne soirée