Un système d'inégalités

[Dacu]

Bonjour à tous,

Résoudre le système d'inégalités:

, où .

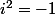
Cordialement,

Dacu

[pascal16]

les équations n'ont pas de sens, il faut définir une relation d'ordre
x et y sont des réels ou des complexe ou des schmilblicks (nombres complexes ordonnés) ?

[Pseuda]

Bonjour,

On pose x=a+ib, y=c+id, avec a,b,c,d réels. Les inégalités sont vérifiées à la condition supplémentaire que les membres de gauche soient réels. Sauf erreur, j'ai trouvé les solutions, mais je laisse les autres chercher ce problème intéressant .

[NicoTial]

J'ai également trouvé des solutions... mais ce problème m'a beaucoup surpris... il fallait préciser que x et y étaient complexes !

[Pseuda]

C'est le but des problèmes posés par notre ami Dacu : surprendre.

Il faut parfois aussi faire les questions et les réponses.

[NicoTial]

Mais Dacu, tu as réussi ou pas ?

[zygomatique]

salut

à nouveau ce système n'a pas de sens tant qu'on ne sait pas où vivent x et y ...

[Razes]

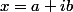
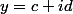
Tel que c'est posé, c'est insensé. A moins de remplacer et et de faire en sorte que les parties imaginaires soient nulles.




Continuez

[Dacu]

Mais Dacu, tu as réussi ou pas ?

Bonjour,

Mon raisonnement:

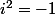
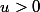
Nous pouvons écrire que , où et , , ....et donc on obtient ainsi un système d'équations qui peut être résolu facilement...

Cordialement,

Dacu

[NicoTial]

Mais Dacu, tu as réussi ou pas ?

Bonjour,

Mon raisonnement:

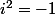
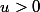
Nous pouvons écrire que , où et , , ....et donc on obtient ainsi un système d'équations qui peut être résolu facilement...

Cordialement,

Dacu

Regarde plutôt la méthode de Razès, c'est comme ça que j'ai fait aussi

[zygomatique]

ça n'a pas de sens ... d'écrire une inégalité avec un nombre complexe ...

[Arbre]

Bonjour,

@Zyg : Encore faut-il faire preuve d'un peu de bonne volonté comme cela est nécéssaire pour n'importe quelle énoncé mathématiques, avec de la mauvaise volonté on peut faire mine de ne pas comprendre, les énoncés de maths.

Et en plus on a répondu à ton interrogation avant que tu l'as formule.

Au revoir.

[Dacu]

Mais Dacu, tu as réussi ou pas ?

Bonjour,

Mon raisonnement:

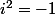
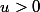
Nous pouvons écrire que , où et , , ....et donc on obtient ainsi un système d'équations qui peut être résolu facilement...

Cordialement,

Dacu

Regarde plutôt la méthode de Razès, c'est comme ça que j'ai fait aussi

Bonjour,

Il est très bon et le raisonnement de Razès....Mon raisonnement est bon?

Cordialement,

Dacu

[MJoe]

Bonjour à tous,

D'accord avec @zygomatique, écrire des inégalités avec des complexes, c'est bizarre. Ou alors il faut ajouter d'autres conditions.
Au début je pensais à ce type de système (avec des modules) :



MJoe.

[NicoTial]

Bonjour,

Mon raisonnement:

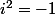
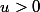
Nous pouvons écrire que , où et , , ....et donc on obtient ainsi un système d'équations qui peut être résolu facilement...

Cordialement,

Dacu

Regarde plutôt la méthode de Razès, c'est comme ça que j'ai fait aussi

Bonjour,

Il est très bon et le raisonnement de Razès....Mon raisonnement est bon?

Cordialement,

Dacu

Je ne comprends pas ton raisonnement... qui est u et v ?

[NicoTial]

Bonjour à tous,

D'accord avec @zygomatique, écrire des inégalités avec des complexes, c'est bizarre. Ou alors il faut ajouter d'autres conditions.
Au début je pensais à ce type de système (avec des modules) :



MJoe.

Justement, les conditions non précisées sont évidentes : il faut annuler les parties imaginaires pour obtenir des nombres réels finalement.

[Arbre]

Bonjour,

@MJoe : c'est comme quand on écrit cela veux dire

[zygomatique]

MDR ...

si le contexte ne précise pas que M est réel alors à nouveau ça n'a pas de sens ...

mais on t'a repris déjà tellement de fois (Ben314 entre autre) et tu continues ...

il n'est pas question de bonne volonté ou d'interprétation, il est question et surtout dans un énoncé de préciser exactement et précisément la situation : et surtout le domaine de définition de toutes les variables ...

Bonjour,

@Zyg : Encore faut-il faire preuve d'un peu de bonne volonté comme cela est nécessaire pour n'importe quelle énoncé mathématiques, avec de la mauvaise volonté on peut faire mine de ne pas comprendre, les énoncés de maths.

Et en plus on a répondu à ton interrogation avant que tu l'as formule. ... tu la formules ...

Au revoir.

non justement ... comme il est dit au-dessus ...

[Arbre]

il n'est pas question de bonne volonté ou d'interprétation, il est question et surtout dans un énoncé de préciser exactement et précisément la situation : et surtout le domaine de définition de toutes les variables ...

Ok, peux-tu donner un énoncé où l'on a pas besoin de faire preuve de bonne volonté pour le comprendre, pour voir de quoi tu parles.

J'en avais déjà discuté ici :
cafe-mathematique/imaginer-dans-notre-monde-t185657-20.html

[Dacu]

Je ne comprends pas ton raisonnement... qui est u et v ?

Bonjour,
Une inégalité peut être transformé en une équation?Je dis , oui!
Comme je l'ai écrit dans mon raisonnement .Enfin, les solutions sont les suivantes:
et qui sont les mêmes que celles données par Razès.S'il vous plaît vérifier!

Cordialement,

Dacu