Système d'équations (exo classique)

par **Kurt Gödel** » 20 Sep 2009, 10:01

Bonjour,

Je dois résoudre dans C le système:

Je suis parvenu à montrer que

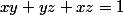
, ensuite je veux montrer que

,

et

sont les racines complexes de l'équation

, mais je ne vois pas comment faire.

Merci d'avance

par **girdav** » 20 Sep 2009, 10:04

Bonjour.
Tu peux écrire

, développer le membre de gauche et identifier.

par **Kurt Gödel** » 20 Sep 2009, 10:59

Merci beaucoup!

par **Kurt Gödel** » 20 Sep 2009, 15:24

Au fait, comment puis-je démontrer que mon système d'équations est équivalente à cette équation du 3ème degré?

Merci d'avance.

par **girdav** » 20 Sep 2009, 15:44

On montre que les racines de l'équation vérifient

Il ne te reste plus qu'à montrer que le système de départ est équivalent à celui-ci.

par **Kurt Gödel** » 20 Sep 2009, 16:22

D'accord, merci beaucoup girdav!

J'ai une autre question, aucun rapport avec cet exo dessus:

Soit E et F des ensembles, f une application de E vers F et A une partie de E

1) Montrer que

Ok pas de problème

2) Montrer que:
Pour toute partie A de E,

injective
Là je bloque: j'ai fait le sens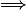

. Et pour le sens

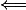, je veux procéder par double inclusion (la première inclusion est dans la question 1), donc il me reste à montrer que f injective

. Et là j'ai besoin d'aide.

Merci

par **Kurt Gödel** » 20 Sep 2009, 18:34

Merci infiniment!

par **yos** » 20 Sep 2009, 19:12

Kurt Gödel a écrit:Je suis parvenu à montrer que

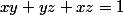
facilement?

Système d'équations (exo classique)

Système d'équations (exo classique)

Qui est en ligne