Bonjour,
Je cherche à résoudre le système suivant d'équations différentielles non linéaires pour la simulation d'un problème de physique:
du/dt=f(t,u,v,w)
dv/dt=f(t,u,v,w)
dw/dt=f(t,u,v,w)
(A,B,K1,K2,K3,g) des constantes.
J'envisage d'utiliser une méthode numérique. Je me suis déjà servi de la méthode Runge-kutta d'ordre 4 qui m'arrange bien niveau précision mais je n'arrive pas à adapter son algorithme à un système (si ça se fait :hein: ). Vu que le problème est non linéaire, il n'est pas possible de le mettre sous forme matricielle pour se ramener à une seule équation,du coup je bloque. Le même problème se pose avec les autres méthodes que je connais mais moins précises (Euler,demi-point).
Déja, j'ai simplifié le problème (passer de l'ordre2 à 1): ici je cherche à obtenir les vitesses bien que ce soit les positions x,y,z qui mintéressent, une simple intégration numérique me permettra de retrouver ces derniers :zen:.
Merci d'avance pour toute aide et proposition
Système d'équations différentielles non linéaires (résolution numérique)
3 messages
- Page 1 sur 1
méthode d'euler pour commencer
re-bonjour,
voici pour aider un algorithme pour la méthode d'Euler plus simple que Runge-Kutta:
À partir du point initial ( x0 , y0 ), on applique la formule d'itération suivante, pour m allant de 0 à n - 1 :
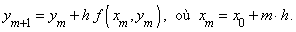
avec h le pas de discrétisation.
c'est facile à appliquer dans le cas où il n'y a pas de système.
voici pour aider un algorithme pour la méthode d'Euler plus simple que Runge-Kutta:
À partir du point initial ( x0 , y0 ), on applique la formule d'itération suivante, pour m allant de 0 à n - 1 :
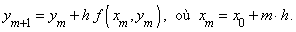
avec h le pas de discrétisation.
c'est facile à appliquer dans le cas où il n'y a pas de système.
firefighter90 a écrit:re-bonjour,
voici pour aider un algorithme pour la méthode d'Euler plus simple que Runge-Kutta:
À partir du point initial ( x0 , y0 ), on applique la formule d'itération suivante, pour m allant de 0 à n - 1 :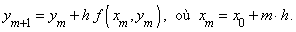
avec h le pas de discrétisation.
c'est facile à appliquer dans le cas où il n'y a pas de système.
trouvé
ici le "X" c'est "t" et "Y" c'est le vecteur [u,v,w].
donc dans chaque itération, il y a trois nouveau "Ym" et un nouvel "Xm" :zen:
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
