Un système d'équations avec des modules de fonction
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 09 Sep 2016, 13:03
par Razes » 09 Sep 2016, 13:03
Razes a écrit:@zygomatique Juste un petit bémol, tu as oublié une petite équation mais ayant une grande incidence.
+3g'(x)|=3-x\\ |3g(x)-f'(x)|=x-3 \end{matrix}\right.\Rightarrow \left\{\begin{matrix}x-3=0\\ f(x) + 3g'(x) = 0\\ 3g(x) - f'(x)=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix}x=3\\ f(3) + 3g'(3) = 0\\ 3g(3) - f'(3)=0\end{matrix}\right.)
Nous n'avons plus rien à résoudre après.
Vous vous cassez la tête, tel que l'énoncé est posé il n y a pas de système à résoudre et pas de fonction à trouver.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 09 Sep 2016, 17:23
par Dacu » 09 Sep 2016, 17:23
Pseuda a écrit:Bonjour,
Ah Dacu ...
Pour ma part, je dirais :
 + 3 g'(x) | = 3 -x \Rightarrow)
la fonction

n'est définie que sur ]-

, 3]
 - f'(x) | = x-3 \Rightarrow)
la fonction

n'est définie que sur [3,

[
Donc le domaine de définition commun à ces 2 fonctions est {3}, mais je suis bloquée là.
Bonsoir,
Lire tous mes messages sur ce sujet et vous débloquerez ....

Qu'est-ce que ce n'est pas clair?
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 09 Sep 2016, 19:36
par zygomatique » 09 Sep 2016, 19:36
je ne suis pas tout à fait d'accord avec pseuda ... enfin je pense qu'il dit mal les choses ...
si les fonctions sont définies sur R alors pour tout x différent de 3 on aboutit à une contradiction
si x <> 3 alors x - 3 et 3 - x sont opposés et non nuls donc l'une des deux équations n'a pas de solution ...
or l'ensemble des solutions d'un système d'équations est l'intersection des ensembles de solutions de chaque équation ...
et l'ensemble vide est absorbant pour l'opération d'intersection ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 09 Sep 2016, 19:59
par Razes » 09 Sep 2016, 19:59
Vous vous cassez la tête, tel que l'énoncé est posé il n y a pas de système à résoudre et pas de fonction à trouver.
Le plus simple est de faire une démonstration par "l'absurde" (façon de parler).
Supposons que Pseuda et Dacu ont raison (ne me dites pas que je suis de mauvaise fois mais allons jusqu'au bout des choses pour qu'on soit fixés une fois pour toutes), personnellement je pense que tout un chacun peut faire des erreurs et il m'importe de connaitre mon erreur.
Résolvons le système d'équations, déterminons

et

et vérifions la consigne. A priori le système sans valeur absolue est vraiment très facile. il est du type:
-f"(x)=0\\ g(x)+g"(x)=0\end{matrix}\right.)
Je n'ai pas calculé le second membre.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Sep 2016, 05:47
par Dacu » 10 Sep 2016, 05:47
zygomatique a écrit:je ne suis pas tout à fait d'accord avec pseuda ... enfin je pense qu'il dit mal les choses ...
si les fonctions sont définies sur R alors pour tout x différent de 3 on aboutit à une contradiction
si x <> 3 alors x - 3 et 3 - x sont opposés et non nuls donc l'une des deux équations n'a pas de solution ...
or l'ensemble des solutions d'un système d'équations est l'intersection des ensembles de solutions de chaque équation ...
et l'ensemble vide est absorbant pour l'opération d'intersection ...
Bon matin,
Le système initial d'équations différentielles a quatre paires de solutions en vertu la définition d'un module de nombre réel qui sont donnés par les quatre systèmes d'équations différentielles:
1)
+3g'(x)=3-x\\ 3g(x)-f'(x)=x-3\\ \end{array})
2)
+3g'(x)=3-x\\ -3g(x)+f'(x)=x-3\\ \end{array})
3)
-3g'(x)=3-x\\ -f'(x)+3g(x)=x-3\\ \end{array})
4)
-3g'(x)=3-x\\ f'(x)-3g(x)=x-3\\ \end{array})
.
Toutes ces solutions vérifier système initial d'équations différentielles ....

----------------------------------------------------
Je vous dis ce qu'il a dit EUCLID:
,,Ce qui est affirmé sans preuve peut être nié sans preuve. "Cordialement et à bientôt....
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Sep 2016, 10:13
par zygomatique » 10 Sep 2016, 10:13
mais bon sang de bonsoir
1/ où sont définies f et g ?
2/ parler de f' et g' signifie donc que f et g sont dérivables (donc continues entre autre)
3/
+3g'(x)|=3-x\\ |3g(x)-f'(x)|=x-3\\ \end{array})
donc pour x = 2 on obtient :
 + 3g'(2)| = 1 \\ |3g(2) - f'(2)|= -1 \\ \end{array})
et pour x = 4 on obtient :
 + 3g'(4)| = -1 \\ |3g(4) - f'(4)|= 1 \\ \end{array})
4/ parler du module d'un réel .... me laisse perplexe ...
conclusion :
a/ tu nous présentes la résolution des quatre systèmes
b/ tu nous montres que les couples (f, g) de solutions sont solution du système initial
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Sep 2016, 10:26
par Razes » 10 Sep 2016, 10:26
Dacu a écrit:1)
+3g'(x)=3-x\\ 3g(x)-f'(x)=x-3\\ \end{array})
----------------------------------------------------
Je vous dis ce qu'il a dit EUCLID:
,,Ce qui est affirmé sans preuve peut être nié sans preuve. "
EUCLID c'est la devise
zygomatique , pas de soucis de ce coté.
Comme demanderait EUCLID, cherchons la solution du système n°1. Il est facile.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Sep 2016, 11:39
par Dacu » 10 Sep 2016, 11:39
zygomatique a écrit:mais bon sang de bonsoir
3/
+3g'(x)|=3-x\\ |3g(x)-f'(x)|=x-3\\ \end{array})
donc pour x = 2 on obtient :
 + 3g'(2)| = 1 \\ |3g(2) - f'(2)|= -1 \\ \end{array})
et pour x = 4 on obtient :
 + 3g'(4)| = -1 \\ |3g(4) - f'(4)|= 1 \\ \end{array})
4/ parler du module d'un réel .... me laisse perplexe ...
conclusion :
a/ tu nous présentes la résolution des quatre systèmes
b/ tu nous montres que les couples (f, g) de solutions sont solution du système initial
Je dis encore une fois:
Vérifier , par exemple ,
=3c_1\sin{x}+c_2\cos{x}-x+2)
et
=c_1\cos{x}-\frac{1}{3}c_2\sin{x}+\frac{x-4}{3})
.Remplacer ces fonctions en le system initial nous obtenons
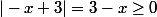
et
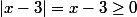
et ce qui est vrai....Il est clair maintenant?Quelle est la définition d'un module de nombre réel????

Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Sep 2016, 12:13
par Razes » 10 Sep 2016, 12:13
@Dacu
Ne nous dispersons pas. Résolvons le système N°1 jusqu'au bout.
Ce dont nous avons besoin, c'est de l'énoncé initial:
+3g'(x)|=3-x\\ |3g(x)-f'(x)|=x-3\\ \end{array})
.
En plus du système suivant que tu as proposé.
1)
+3g'(x)=3-x\\ 3g(x)-f'(x)=x-3\\ \end{array}) Important:
Important: Si tu enlève une valeur absolue, tu précise le domaine dans lequel on travaille.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Sep 2016, 13:38
par Dacu » 10 Sep 2016, 13:38
Razes a écrit:@Dacu
Ne nous dispersons pas. Résolvons le système N°1 jusqu'au bout.
Ce dont nous avons besoin, c'est de l'énoncé initial:
+3g'(x)|=3-x\\ |3g(x)-f'(x)|=x-3\\ \end{array})
.
En plus du système suivant que tu as proposé.
1)
+3g'(x)=3-x\\ 3g(x)-f'(x)=x-3\\ \end{array}) Important:
Important: Si tu enlève une valeur absolue, tu précise le domaine dans lequel on travaille.
Bonjour,
Pour le caz 1) nous avons:
+3g'(x)|=f(x)+3g'(x))
pour
+3g'(x)\geq 0)
-f'(x)|=3g(x)-f'(x))
pour
-f'(x)\geq 0)
--------------------------------------------------
Il est nécessaire de trouver les fonctions
)
et
)
et non pas les valeurs de

, mais il est évident qu'en ce système d'équations différentielles il faut en généralement
|=p\geq 0)
...qui ne nécessite pas de trouver les fonctions
)
et
)
....Trouver les valeurs de

pour
+3g'(x)\geq 0)
et pour
-f'(x)\geq 0)
, est une autre problème...

Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Sep 2016, 14:27
par Razes » 10 Sep 2016, 14:27
@Dacu
Tous ça est improductif, on tourne en rond. Le système suivant que tu as proposé.
1)
+3g'(x)=3-x\\ 3g(x)-f'(x)=x-3\\ \end{array})
Nous conduit à un système
supplémentaire facile à résoudre:
+f''(x)=2-x\\ 3(g(x)+g''(x))=x-4\\ \end{array})
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Sep 2016, 15:11
par Dacu » 10 Sep 2016, 15:11
Razes a écrit:@Dacu
Tous ça est improductif, on tourne en rond. Le système suivant que tu as proposé.
1)
+3g'(x)=3-x\\ 3g(x)-f'(x)=x-3\\ \end{array})
Nous conduit à un système
supplémentaire facile à résoudre:
+f''(x)=2-x\\ 3(g(x)+g''(x))=x-4\\ \end{array})
Très bien!Enfin, il y a les fonctions
)
et
)
qui vérifie le système initial d'équations différentielles.J'espère que maintenant tout est clair...

Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Sep 2016, 16:04
par Razes » 10 Sep 2016, 16:04
Ne te réjouis pas trop tôt.
Non, Dacu, on n'a pas encore trouvé les fonctions et on n'a pas encore vérifié le système initial.
A toi de terminer, je t'ai simplifié beaucoup les choses.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Sep 2016, 17:38
par zygomatique » 10 Sep 2016, 17:38
Dacu a écrit: Razes a écrit:@Dacu
Tous ça est improductif, on tourne en rond. Le système suivant que tu as proposé.
1)
+3g'(x)=3-x\\ 3g(x)-f'(x)=x-3\\ \end{array})
Nous conduit à un système
supplémentaire facile à résoudre:
+f''(x)=2-x\\ 3(g(x)+g''(x))=x-4\\ \end{array})
Très bien!Enfin, il y a les fonctions
)
et
)
qui vérifie le système initial d'équations différentielles.J'espère que maintenant tout est clair...

MDR zygomatique a écrit:mais bon sang de bonsoir
1/ où sont définies f et g ?
2/ parler de f' et g' signifie donc que f et g sont dérivables (donc continues entre autre)
3/
+3g'(x)|=3-x\\ |3g(x)-f'(x)|=x-3\\ \end{array})
donc pour x = 2 on obtient :
 + 3g'(2)| = 1 \\ |3g(2) - f'(2)|= -1 \\ \end{array})
et pour x = 4 on obtient :
 + 3g'(4)| = -1 \\ |3g(4) - f'(4)|= 1 \\ \end{array})
4/ parler du module d'un réel .... me laisse perplexe ...
conclusion :
a/ tu nous présentes la résolution des quatre systèmes
b/ tu nous montres que les couples (f, g) de solutions sont solution du système initial
j'ai pris 2 comme j'aurai pu prendre n'importe quel réel strictement inférieur à 3
j'ai pris 4 comme j'aurai pu prendre n'importe quel réel strictement supérieur à 3
j'attends une réponse à 1/ ....
prenons les fonctions que tu nous donnes dans un de tes précédents posts ::
 = a \cos x + 3b \sin x - x + 2)
 = b \cos x - \dfrac a 3 \sin x + \dfrac 1 3 (x - 4))
 = -a \sin x + 3b \cos x - 1)
 = -b \sin x - \dfrac a 3 \cos x + \dfrac 1 3)
 + 3g'(x) = -x + 2 + 1 = 3 - x)
 - f'(x) = x - 4 + 1 = x - 3) MDR
MDRet maintenant si tu mets une valeur absolue au membre de gauche que se passe-t-il ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Sep 2016, 19:14
par Dacu » 10 Sep 2016, 19:14
Razes a écrit:Ne te réjouis pas trop tôt.
Non, Dacu, on n'a pas encore trouvé les fonctions et on n'a pas encore vérifié le système initial.
A toi de terminer, je t'ai simplifié beaucoup les choses.
Bonsoir,
J'attends , avec intérêt , vos calculs.
Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 10 Sep 2016, 19:23
par Dacu » 10 Sep 2016, 19:23
zygomatique a écrit:MDR
Bonsoir,
Qu'est-ce que
,,MDR"????

Je pense qu'il serait préférable de demander à un professeur pour expliquer à résoudre ce problème ...

Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 10 Sep 2016, 19:34
par zygomatique » 10 Sep 2016, 19:34
Mort De Rire ...
j'ai résolu le pb ... et tu ne t'en rends pas compte ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Razes
- Membre Rationnel
- Messages: 964
- Enregistré le: 28 Juil 2014, 19:24
-
 par Razes » 10 Sep 2016, 19:45
par Razes » 10 Sep 2016, 19:45
Quelle perte de temps!
@Dacu
Tu as balancé un truc faux en contredisant le bon sens, je t'ai proposé de t'aider pour résoudre le système même si le résultat me donnera tort, tu n'a même été capable de nous faire avance d'un petit pas.
Pour clore le sujet. Est tu capable de résoudre le système suivant:
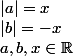
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 11 Sep 2016, 08:27
par Dacu » 11 Sep 2016, 08:27
Razes a écrit:Quelle perte de temps!
@Dacu
Tu as balancé un truc faux en contredisant le bon sens, je t'ai proposé de t'aider pour résoudre le système même si le résultat me donnera tort, tu n'a même été capable de nous faire avance d'un petit pas.
Pour clore le sujet. Est tu capable de résoudre le système suivant:
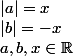
Bon matin,
Vraiment,quelle perte de temps......

Si

sont des nombres , alors
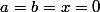
, mais si par exemple ,
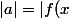+3g'(x)|=x)
et
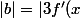-g(x)|=-x)
, alors nous avons un autre problème qui a de multiples solutions...

Cordialement!
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 11 Sep 2016, 12:11
par Pseuda » 11 Sep 2016, 12:11
Bonjour,
Mais Dacu enfin, zygomatique a démontré depuis longtemps que ce système n'a pas de solution.
On aboutit à ce que les fonctions f et g et leurs dérivées f' et g' ne sont définies qu'en 3, ce qui est impossible : pour être dérivable en un point, une fonction doit être définie au moins sur un intervalle contenant ce point.
D'ailleurs, les fonctions que tu proposes avec des sin et des cos sont définies sur R.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
